写给你的因子投资
00 引言
到底什么是因子投资?因子投资涵盖的内容包罗万象 。有人用因子来获取收益,也有人用因子来控制风险;有人用因子进行被动的资产配置,也有人用因子博取主动的套利收益;有人用因子研究预期收益率,也有人用因子研究收益率的波动……这些差异性的使用方式足以把刚接触因子投资的人搞得晕头转向 。
如果将“什么是因子投资”这个问题抛给从事因子投资的人 , 一千个人也可能给出一千种答案 。因子投资涉及的内容虽然看似纷繁 , 但它们其实非常协调地构成了一个有机的整体 。
如何站在一个统一视角下探讨因子投资的方方面面呢?
01 一个公式
20 世纪 60 年代,资本资产定价模型(Capital Asset Pricing Model,即 CAPM)问世,首次清晰地描绘出风险和收益率之间的关系 。根据 CAPM 理论,资产的预期超额收益由下面这个一元线性模型决定: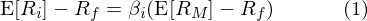
其中 E[.] 是期望符号,R_i 为某资产 i 的收益率,R_f 为无风险收益率,R_M 为市场组合的收益率 。式中 β_i = cov(R_i, R_M)/var(R_M) 刻画了该资产收益对市场收益的敏感程度,它也被称为资产 i 对市场风险的暴露程度 。CAPM 正是最简单的线性因子模型,它指出资产的预期超额收益率由市场组合的预期超额收益率和资产对市场风险的暴露大小决定,而市场组合也被称为市场因子 。
公式 (1) 这个简单的关系为后续大量线性多因子定价模型的研究拉开了序幕 。人们发现不同资产的收益率并非由单一的市场因子决定,而是同时受到其他因子的影响 。以此为契机,Ross (1976) 提出了著名的套利定价理论(Arbitrage Pricing Theory , 简称 APT),在 CAPM 的基础上做了进一步延伸,构建了线性多因子定价模型(简称多因子模型) 。多因子模型假设资产 i 的预期超额收益由以下多元线性模型决定:
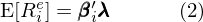
其中 E[R_i^e] 表示资产 i 的预期超额收益 , β_i 是资产 i 的因子暴露(factor exposure)或称因子载荷(factor loading),λ 是因子预期收益(factor expected return)、也常被称为因子溢价(factor risk premium) 。式 (2) 中引入符号 E[R_i^e] 代表预期超额收益而舍弃了 E[R_i] - R_f,原因如下 。对于个股或者由若干支股票组成的纯多头投资组合这类资产,它的预期超额收益是 E[R_i] 和无风险收益率 R_f 之差,即 E[R_i] - R_f 。在实证资产定价中 , 另一类常见的资产是通过多空对冲构建的资金中性投资组合 , 例如做多一定金额的股票、同时做空同样金额的股票 。依照定义,这类资产的预期超额收益率就是多头和空头预期收益之差 , 无需额外减去无风险收益率 。因此,使用 E[R_i^e] 代表资产的预期超额收益更具一般性 。
和 CAPM 类似,多因子模型假设 E[R_i^e] 由 (2) 式右侧的一系列因子的预期收益率和资产在这些因子上的暴露决定 。它表明多因子模型研究的是不同资产预期收益率之间的差异,而非单一资产收益率在时序上的变化 。在多因子模型研究的术语中,不同资产预期收益率的差异通常被称为(横)截面(cross-sectional)差异 , 资产预期收益率的高低由它在这些因子上的暴露 β_i 大小决定 。
多因子模型在数学上简单、优雅,它允许人们在公式 (2) 的右侧加上任何可能影响资产预期收益率的因子 。然而,实际的金融市场十分复杂,影响资产收益率的原因层出不穷又千变万化 。因此 , 虽然 (2) 给出了市场均衡状态下资产的预期收益率,但在实际中其左、右两侧往往并不相等,而是存在一个定价误差(pricing error):
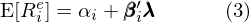
上式中 α_i 是资产 i 的实际预期收益率和多因子模型隐含的预期收益率之间的定价误差 。该误差背后的原因可以从以下两方面来考虑:
1. 模型设定偏误,即公式 (2) 右侧遗漏了重要的因子 。当被遗漏的因子被加入后,即可消除误差 。
2. 模型本身没有问题 , 但由于资产收益率的实际数据仅仅是总体的一个样本 , 因此误差总是存在的 。这时需要通过统计方法检验误差 α_i 是否显著不为零:
- 2.1 如果 α_i 并非显著的偏离零,那么可以认为它的出现仅仅是因为运气的原因;
- 2.2 如果 α_i 显著偏离零,它则代表了某个可以通过套利而获得超额收益的机会;它也同时说明由于某些原因,市场对该资产出现错误定价(mispricing) , 从而导致其实际预期收益率和模型下的预期收益率出现了偏离 。
作为当今一个重要的投资类别 , 因子投资中涉及的内容非常丰富 , 但所有的方面都可以围绕公式 (3) 来展开和讨论,形成关于因子投资的统一视角 。
02 因子、多因子模型、异象
下图展示了 (3) 中的三个成分 。在多因子模型中 , β'_iλ 中包含了多个影响 (3) 左侧资产收益率的解释变量,每个解释变量代表了一个因子 。多个因子的预期收益率以及资产在它们上的暴露放在一起构成的 β'_iλ 就是多因子模型 。对于某个给定的资产 i,如果它的实际预期收益率和多因子模型隐含的预期收益率之间的误差 α_i 显著不为零,则称这个资产为一个异象(anomaly) 。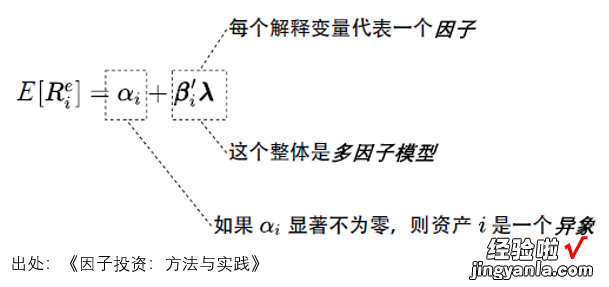
因子投资中最重要自然是因子 。那么 , 因子到底是什么?如何选择因子?由 (3) 可知,它左侧不同资产的收益率均可以归结到有限个因子的收益率上,而不同资产预期收益率的高低由它们对因子的暴露大小决定 。由此可以得出因子的定义:
