小知识之同心椭圆和圆公切线段长度问题
与圆锥曲线相关的切线问题是高考中的常见题型了,如何设点,如何快速写出切线方程以及与抛物线有关的切线常见结论已经在公众号中出现多次了 , 文末也会给出相关的扩展链接,近期遇到一个这样的题目,如下:
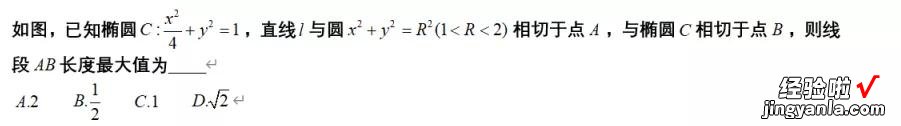
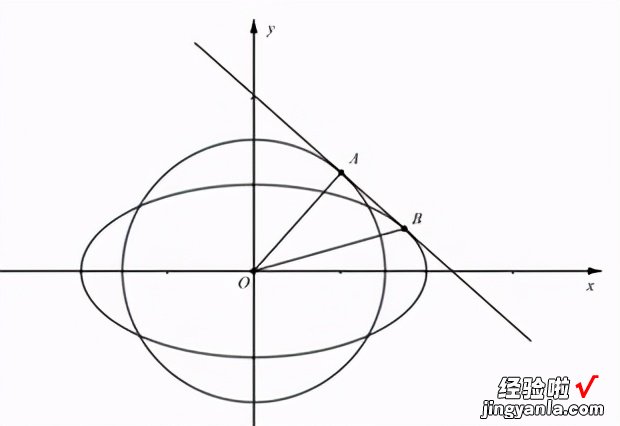
很显然题目中的变量是R,在直角三角形OAB中,只需用R表示出OB的长度即可 , 设切线为y=kx m,求出点B的坐标 , 坐标中含有k,m,再转化为只含有R的坐标即可,用勾股定理求出AB的最大值,题目不难,过程如下:

上题中,当存在k,m,R三个变量时,线段的长度最大值为一个常数 , 虽然三个变量可转化为一个变量,最值是根据不等式得来,但本题目中a=2,b=1,最大值为1,正好是a-b的值,其实本题的原型题目是2014年浙江的高考题,关于线段距离的最大值为a-b的证明过程如下:

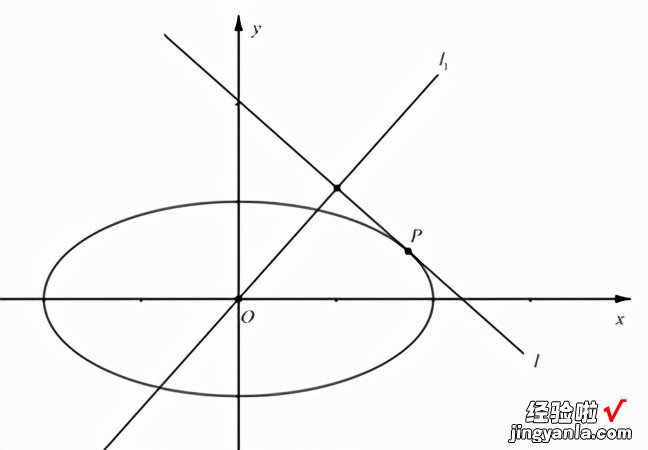
题目和上题类似,只是不是以同心圆的形式给出的,第一问表示点P的坐标方法可与上题相同,也可根据椭圆的切线方程来求出l的斜率,再联立椭圆方程即可 。
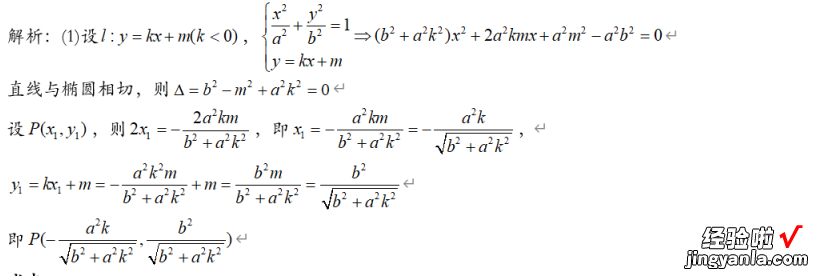
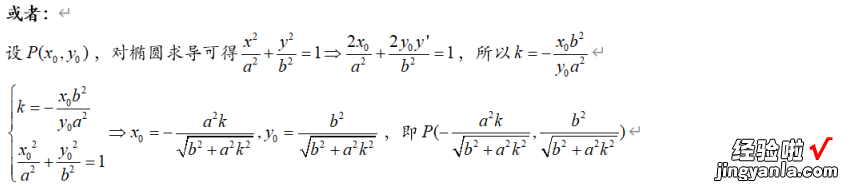
显然求出切线斜率再联立椭圆方程更加简单,但不可出现在大题的步骤中 , 第一问已经表示出点P的坐标,直接利用点到直线的距离即可表示出线段的长度 。

以后可作为一个二级结论来使用,与解析几何中切线有关的内容如下:
圆锥曲线中的双切线问题整理
思维训练37.抛物线中的切线问题
圆的切点弦方程的求法
蒙日圆与圆锥曲线结合的小应用
【小知识之同心椭圆和圆公切线段长度问题】考虑到读者阅读时长问题 , 以后的更新以短篇为主,尽量做到日更 。
