一、一般情况下中位数的求解方法
一般情况下 , 求解中位数的基本方法:先把样本中的所有数据从小到大排列好,若样本容量为奇数 , 则中间的那个数据就是中位数;若样本容量为偶数,则中间的那两个数据的平均数就是中位数 。
例1、如图是根据某校10位高一同学的身高(单位:)画出的茎叶图,其中左边的数字从左到右分别表示学生身高的百位数字和十位数字 , 右边的数字表示学生身高的个位数字,从图中可以得到这10位同学身高的中位数是( )


A.161cm B.162cm C.163cm D.164cm
解:由题意,数据为偶数个,所以根据给定的茎叶图和中位数的定义得 , 数据的中位数为162cm,故选B.
例2、某校高一、高二年级各有7个班参加歌咏比赛,他们得分的茎叶图如图所示,对这组数据分析正确的是()
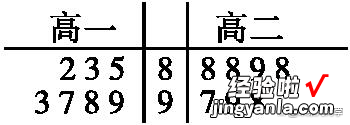
A.高一的中位数大,高二的平均数大
B.高一的平均数大,高二的中位数大
C.高一的平均数、中位数都大
D.高二的平均数、中位数都大
解:由题知,高一高二数据均为奇数个,可直接得出高一的中位数为93,高二为88,选A
由以上例题可见,一般情况下,求解中位数非常简单,只需要看数据是奇数个还是偶数个就好办了 , 那么对于汉频率分布直方图情形下的中位数应该如何求呢?
二、含频率分布直方图中位数的求法
含频率分布直方图的中位数:中位数就是频率分布直方图面积的一半所对应的横坐标 。
这种情形下,求解中位数较为复杂,一般有两种求解方法:
第一种,直接列出算式计算出中位数;
第二种 , 直接设中位数(或其横坐标)为x,然后根据中位数就是频率分布直方图面积的一半所对应的横坐标列出方程 。面积一半时所对应的频率为 。
下面我们以几道题为例,进行详细讲解:

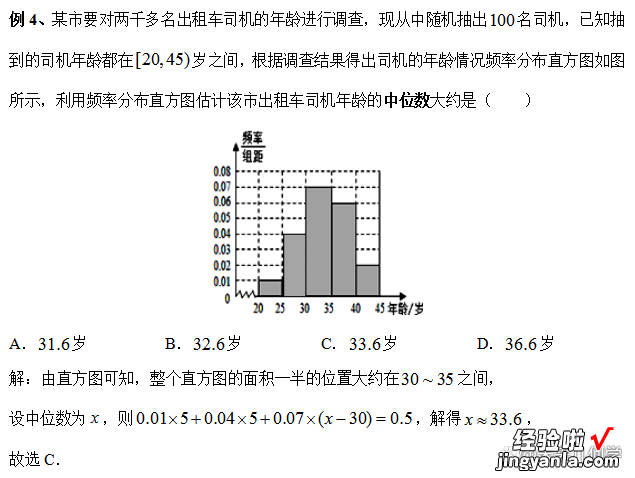
好了 , 今天的内容就分享到这里,如果您有疑问,可以在文章下方留言,欢迎继续关注,精彩还将继续!
【高中数学:含频率分布直方图情形下的中位数怎么求】?
