经验直达:
- 九年级物理的杠杆力臂怎么画
- 杠杆力臂的画法作图
一、九年级物理的杠杆力臂怎么画
一、弹力
1.弹性:物体受力发生形变 , 失去力又恢复到原来的形状的性质叫弹性 。
2.塑性:在受力时发生形变,失去力时不能恢复原来形状的性质叫塑性 。
3.弹力:物体由于发生弹性形变而受到的力叫弹力,弹力的大小与弹性形变的大小有关 。
二、重力
1.重力的概念:地面附近的物体,由于地球的吸引而受的力叫重力 。重力的施力物体是:地球 。
2.重力大小的计算公式G=mg 其中g=9.8N/kg 它表示质量为1kg 的物体所受的重力为9.8N 。
3.重力的方向:竖直向下 。其应用是重垂线、水平仪分别检查墙是否竖直和面是否水平 。
4.重力的作用点——重心:
重力在物体上的作用点叫重心 。质地均匀外形规则物体的重心 , 在它的几何中心上 。如均匀细棒的重心在它的中点,球的重心在球心 。方形薄木板的重心在两条对角线的交点 。
☆假如失去重力将会出现的现象:(只要求写出两种生活中可能发生的)
①抛出去的物体不会下落;②水不会由高处向低处流;③大气不会产生压强 。
三、摩擦力
1.定义:两个互相接触的物体 , 当它们要发生或已发生相对运动时,就会在接触面上产生一种阻碍相对运动的力就叫摩擦力 。
2.分类:。
3.摩擦力的方向:摩擦力的方向与物体相对运动的方向相反 , 有时起阻力作用,有时起动力作用 。
4.静摩擦力大小应通过受力分析,结合二力平衡求得 。
5.在相同条件(压力、接触面粗糙程度相同)下,滚动摩擦比滑动摩擦小得多 。
6.滑动摩擦力:
⑴测量原理:二力平衡条件 。
⑵测量方法:把木块放在水平长木板上 , 用弹簧测力计水平拉木块,使木块匀速运动,读出这时的拉力就等于滑动摩擦力的大小 。
⑶结论:接触面粗糙程度相同时,压力越大滑动摩擦力越大;压力相同时,接触面越粗糙滑动摩擦力越大 。该研究采用了控制变量法 。由前两结论可概括为:滑动摩擦力的大小与压力大小和接触面的粗糙程度有关 。实验还可研究滑动摩擦力的大小与接触面大小、运动速度大小等无关 。
7.应用:
⑴理论上增大摩擦力的方法有:增大压力、接触面变粗糙、变滚动为滑动 。
⑵理论上减小摩擦的方法有:减小压力、使接触面变光滑、变滑动为滚动(滚动轴承)、使接触面彼此分开(加润滑油、气垫、磁悬?。?。
练习:火箭将飞船送入太空,从能量转化的角度来看,是化学能转化为机械能太空飞船在太空中遨游,它受力(“受力”或“不受力”的作用 , 判断依据是:飞船的运动不是做匀速直线运动 。飞船实验室中能使用的仪器是B(A、密度计;B、温度计;C、水银气压计;D、天平) 。
四、杠杆
定义:在力的作用下绕着固定点转动的硬棒叫杠杆 。
说明:①杠杆可直可曲 , 形状任意 。
②有些情况下,可将杠杆实际转一下,来帮助确定支点 。如:鱼杆、铁锹 。
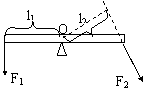
五要素——组成杠杆示意图 。
①支点:杠杆绕着转动的点 。用字母O表示 。
②动力:使杠杆转动的力 。用字母F1表示 。
③阻力:阻碍杠杆转动的力 。用字母F2表示 。
说明:动力、阻力都是杠杆的受力,所以作用点在杠杆上 。
动力、阻力的方向不一定相反,但它们使杠杆的转动的方向相反 。
④动力臂:从支点到动力作用线的距离 。用字母L1表示 。
⑤阻力臂:从支点到阻力作用线的距离 。用字母L2表示 。
画力臂方法:一找支点、二画线、三连距离、四标签 。
⑴找支点O;⑵画力的作用线(虚线);⑶画力臂(虚线,过支点垂直力的作用线作垂线);⑷标力臂(大括号) 。
研究杠杆的平衡条件:
杠杆平衡是指:杠杆静止或匀速转动 。
实验前:应调节杠杆两端的螺母,使杠杆在水平位置平衡 。这样做的目的是:可以方便的从杠杆上量出力臂 。
结论:杠杆的平衡条件(或杠杆原理)是:
动力×动力臂=阻力×阻力臂 。写成公式F1L1=F2L2也可写成:F1 /F2=L2 /L1.
解题指导:分析解决有关杠杆平衡条件问题,必须要画出杠杆示意图;弄清受力与方向和力臂大?。蝗缓蟾菥咛宓那榭鼍咛宸治?nbsp;, 确定如何使用平衡条件解决有关问题 。(如:杠杆转动时施加的动力如何变化,沿什么方向施力最小等 。)
解决杠杆平衡时动力最小问题:此类问题中阻力×阻力臂为一定值,要使动力最小,必须使动力臂最大 , 要使动力臂最大需要做到:①在杠杆上找一点,使这点到支点的距离最远;②动力方向应该是过该点且和该连线垂直的方向 。
4.应用:
名称 结 构特 征 特 点 应用举例
省力
杠杆 动力臂大于阻力臂 省力、费距离 撬棒、铡刀、动滑轮、轮轴、羊角锤、钢丝钳、手推车、花枝剪刀
费力
杠杆 动力臂小于阻力臂 费力、省距离 缝纫机踏板、起重臂、人的前臂、理发剪刀、钓鱼杆
等臂
杠杆 动力臂等于阻力臂 不省力不费力 天平,定滑轮
说明:应根据实际来选择杠杆,当需要较大的力才能解决问题时,应选择省力杠杆,当为了使用方便,省距离时,应选费力杠杆 。
五、滑轮
1.定滑轮:
①定义:中间的轴固定不动的滑轮 。
②实质:定滑轮的实质是:等臂杠杆 。
③特点:使用定滑轮不能省力但是能改变动力的方向 。
④对理想的定滑轮(不计轮轴间摩擦)F=G 。
绳子自由端移动距离SF(或速度vF)=重物移动的距离SG(或速度vG)
2.动滑轮:
①定义:和重物一起移动的滑轮 。(可上下移动,也可左右移动)
②实质:动滑轮的实质是:动力臂为阻力臂2倍的省力杠杆 。
③特点:使用动滑轮能省一半的力,但不能改变动力的方向 。
④理想的动滑轮(不计轴间摩擦和动滑轮重力)则:F= G只忽略轮轴间的摩擦则,拉力F= (G物 G动)绳子自由端移动距离SF(或vF)=2倍的重物移动的距离SG(或vG)
3.滑轮组
①定义:定滑轮、动滑轮组合成滑轮组 。
②特点:使用滑轮组既能省力又能改变动力的方向 。
③理想的滑轮组(不计轮轴间的摩擦和动滑轮的重力)拉力F= G 。只忽略轮轴间的摩擦,则拉力 F= (G物 G动) 。绳子自由端移动距离SF(或vF)=n倍的重物移动的距离SG(或vG) 。
④组装滑轮组方法:首先根据公式n=(G物 G动)/F求出绳子的股数 。然后根据“奇动偶定”的原则 。结合题目的具体要求组装滑轮 。
二、杠杆力臂的画法作图
杠杆力臂的画法是通过图示来表示力臂的长度和方向,以便更好地理解杠杆原理和力的作用效果 。
1.定义杠杆力臂(Definition of Lever Arm)
杠杆力臂是指力作用点到杠杆支点的垂直距离 , 它决定了力对杠杆的作用效果 。在画图时,需要标记出力的作用点和杠杆的支点,并用直线段表示力臂的长度和方向 。

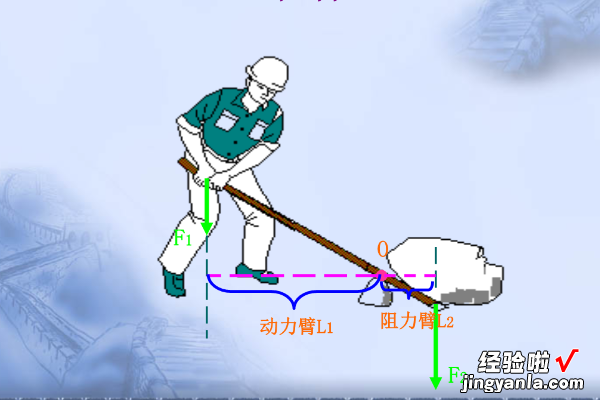
2.画图示例(Example Illustration)
在这个示例中,杠杆的支点是中间的点,上方表示力的作用点,下方表示支点 。通过绘制两个垂直的线段 , 从力作用点到支点的距离就成了力臂 。
3.绘制实际应用中的杠杆(Drawing Levers in Real-life Applications)
在实际应用中,杠杆常常用于各种机械和物理装置中 , 绘制杠杆力臂有助于我们理解力的作用效果 。
例如,在起重机中 , 绘制杠杆力臂有助于确定负载和起重点之间的距离,以及支点和杆的长度 。这样可以计算出所需的力和杆的角度,确保起重机的稳定性和效率 。
4.拓展知识(Expanded Knowledge)
除了画图示例,还可以使用数字和公式来表示杠杆力臂 。力臂的长度可以用垂直距离的测量值表示,也可以使用几何公式来计算 。而在静力学中 , 杠杆力臂对于计算扭矩和平衡条件也非常重要 。扭矩是通过将力乘以力臂来计算的,平衡条件要求扭矩总和为零 。
【杠杆力臂的画法作图 九年级物理的杠杆力臂怎么画】总结起来 , 画出杠杆力臂的图示有助于理解杠杆原理和力的作用效果,同时通过数字和公式表达可以提供更准确的计算和分析 。
