作函数图像的一般步骤是:1、求函数的定义域;2、考察函数的奇偶性、周期性;3、求函数的某些特殊点,如与两个坐标轴的交点 , 不连续点,不可导点等;4、确定函数的单调区间,极值点 , 凸性区间以及拐点;5、考察渐近线;6、画出函数图象 。
下面以作函数f(x)=x^3 6x^2-15x-20的图像为例,来强化一下作函数图像的一般骤 。
分析:1、首先 , 这个函数是定义在R上的 。2、函数既没有奇偶性,也没有周期性 。3、可以求得曲线与x轴有三个交点,与y轴有一个交点 。不存在断点和不可导点 。4、函数有两个稳定点,一个是极大值点,一个是极小值点 。在极大值点的左侧和极小值点的右侧函数单调增,反之单调减 。另外函数有一个拐点,在拐点左侧函数上凸,右侧函数下凸 。5、最后函数并不存在渐近线 。
下面是详细的解题过程 , 不存在的并不做介绍 , 并且有一些地方做了适当的调整:
解:f在R上可导. 【同时说明定义域,连续和可导的性质】
当f(x)=(x 1)(x2 5x-20)=0时, x=-1或x=(-5±根号105)/2;
所以f与x轴有交点(-5-√105,0),(-1,0),(-5 √105,0);
f(0)=-20, f与x轴有交点(0,-20),
当f’(x)=3x^2 12x-15=3(x 5)(x-1)=0时, x=-5或x=1.
当x<-5或x>1时, f’>0, f单调增;当-5
f有极大值点(-5,80), 有极小值点(1,-28).
f”(x)=6x 12, 当x<-2时,f”<0, f凸;当x>-2时, f”>0, f凹.
f有拐点(-2,26).
函数图像的性态如表:

函数图像如图:
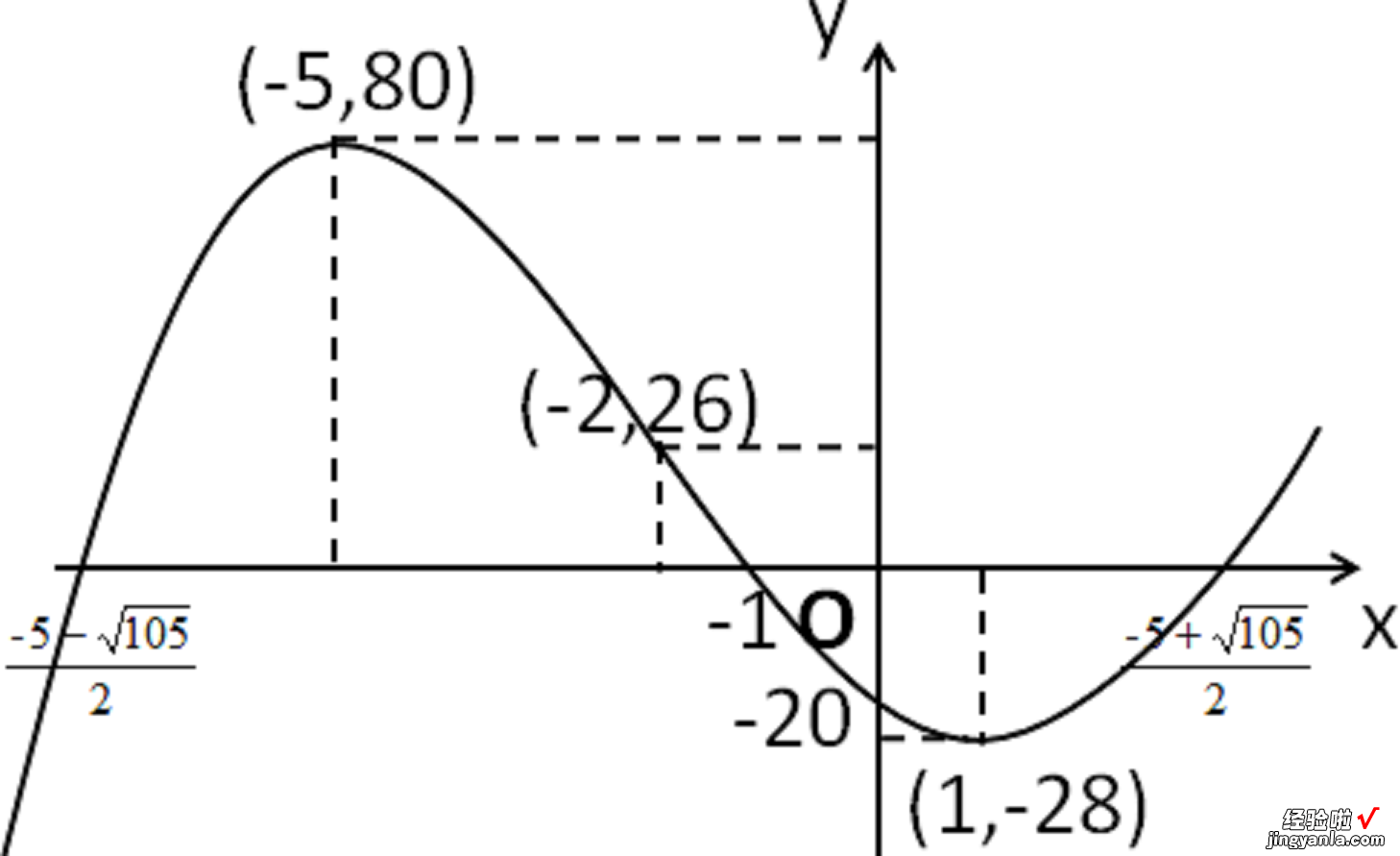
【按函数作图像的一般步骤,作三次函数图像的实例分析】这个图像很难画得准确 。纵轴上的单位长度和横轴上的单位长度的比例是不同的 。这里采用的比例尺,横轴的比例尺几乎是纵轴的比例尺的20倍 。你学会用一般步骤画函数的图像了吗?
