老黄这次要分享的是一个比较复杂的函数图像的画法 , 依然运用画函数图像的一般步骤 。最近老黄比较多地分享了画函数图像的内容 。不知道大家是否有感到一种审美疲劳了呢?战胜这种疲劳感 , 学习才会有更大的进步哦 。
练习:按函数作图的一般步骤,作f(x)=x^(2/3)(x-2)^2的图像.
请自己动手画一画这个函数图像 。
分析:这是一个根式函数和一个二次函数的积,这会导致函数的性状产生比较多的变化 。
1、确定函数的定义域;
这个函数在R上都是有定义的 。
2、考察函数的奇偶性、周期性;
这个函数既不存在奇偶性,也不存在周期性 。
3、求函数的某些特殊点,如与两个坐标轴的交点,不连续点,不可导点等;
【一个比较复杂的函数图像的画法,画函数图像一般步骤的应用】当f(x)=0时 , x=0或x=2,因此,函数过原点,且与x轴有另一个交点(2,0).
4、确定函数的单调区间,极值点,凸性区间以及拐点;
求一阶导数f'(x)=4(2x-1)(x-2)x^(-1/3)/3,可见f(x)在x=0不可导,x=1/2和x=2是函数的两个稳定点 。
由f'(x)的符号性质可知,当x<0或1/2
又由极值第一充分条件可知,函数有极大值点(1/2, 9倍三次根号2 /8),有极小值点(0,0)和(2,0).
又当f"(x)=8(5x^2-5x-1)x^(-4/3) /9=0时, x1=1/2-3根号5 /10, x2=1/2 3根号5 /10.
由f"(x)的符号性质可知,函数x
记y1=f(x1)≈1.45, y2=f(x2)≈0.76, 可知,函数有拐点(x1,y1)和(x2,y2).
5、考察渐近线;
这个函数没有渐近线.

根据上面的信息,将函数图像的性状列表如下:
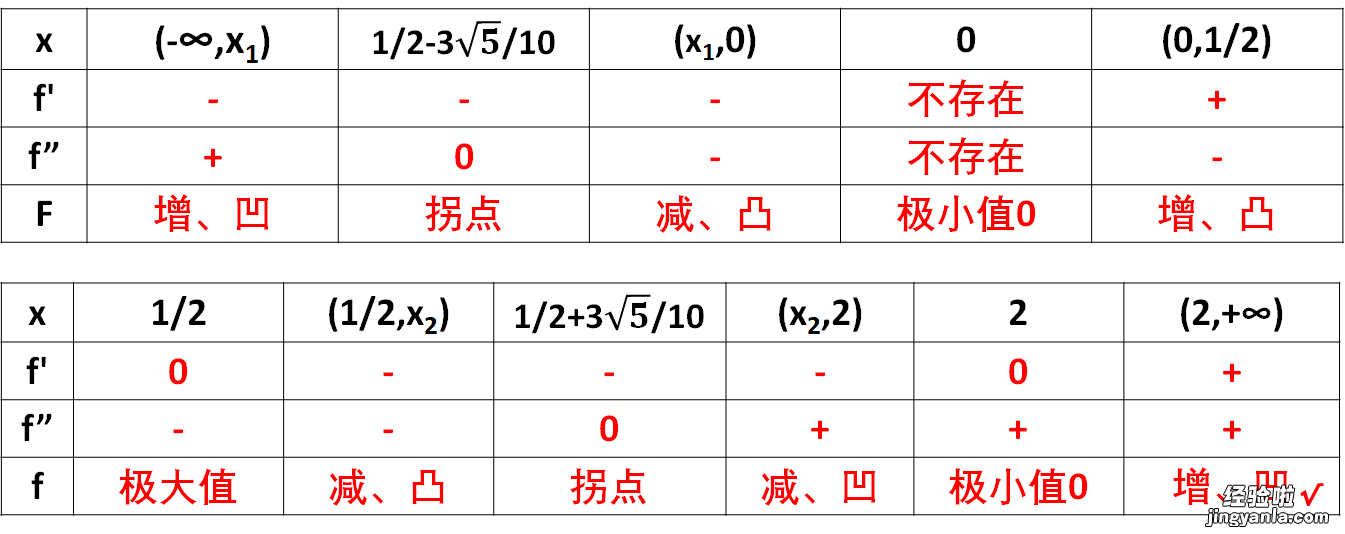
6、画出函数图象 。
最后根据函数的性状,作出函数的图像如下:
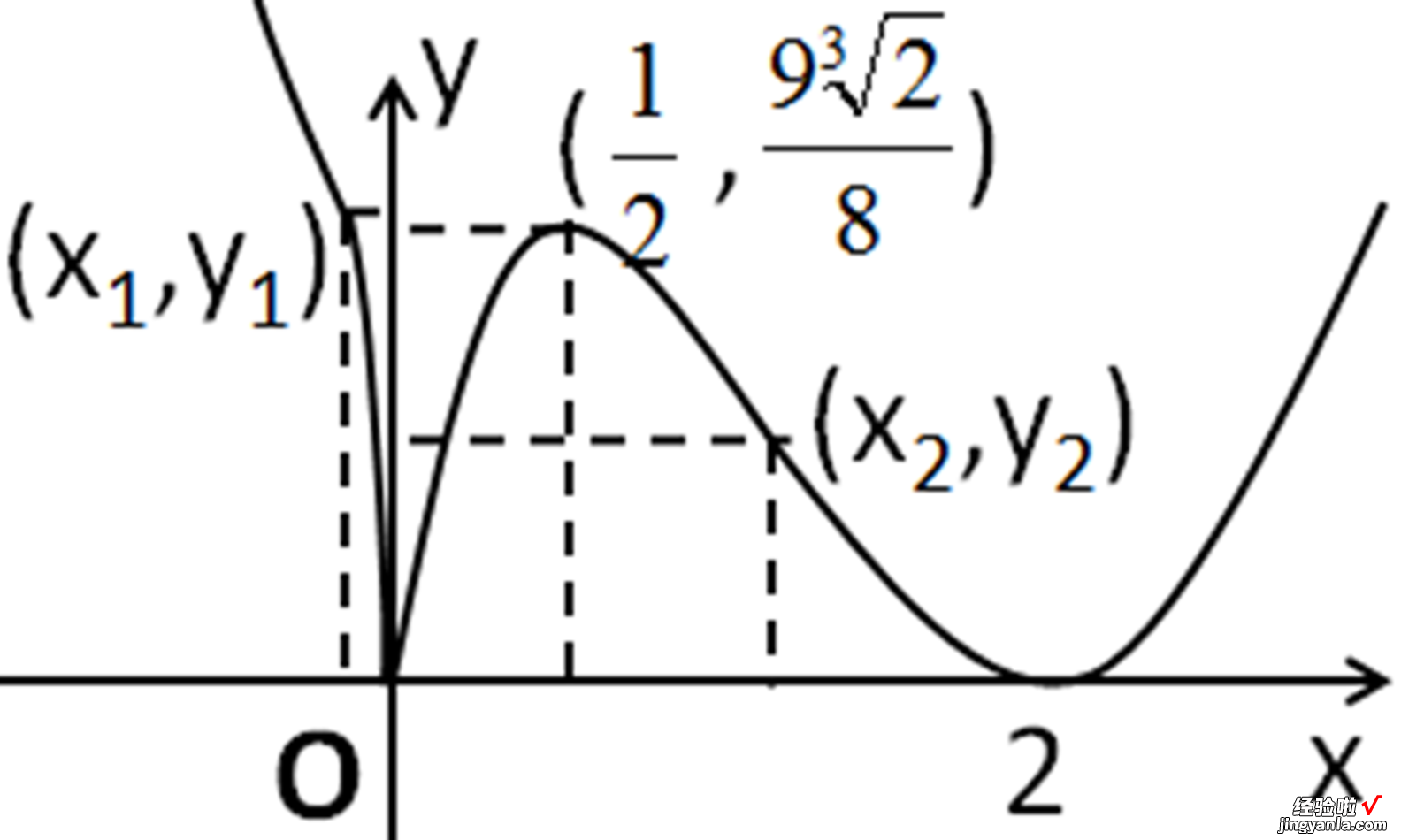
这个图像对低智商的老黄来说 , 还是蛮复杂的 。聪明的你怎么看呢?
