1. SN曲线
S-N曲线是疲劳分析的基?。枋隽瞬牧嫌ατ胙肥倜墓叵?。由于材料的疲劳特性不可避免地存在分散性 , 因此中值S-N曲线实际上不能满足工程设计和疲劳分析的需要,必须考虑疲劳试验的统计特性 。当需要考虑特定失效概率时S-N曲线被称为P-S-N曲线 。
我们将基于某材料的单轴拉伸试验数据进行一次P-S-N曲线的制作 。
2. 试验方法及数据
一般S-N曲线使用单轴拉伸试验数据制作 。单轴疲劳是指材料或零件在单向循环载荷作用下所产生的失效现象 。零件只受单向正应力(应变)或单向切应力(应变),如只承受单向“拉—压”循环应力,弯曲应力或扭转循环应力 。单轴拉伸试验数据使用单轴疲劳试验机施加轴向拉压载荷得出 。

在有限疲劳寿命区采用成组法测试试样的疲劳特性 , 应力分为5级 。因为在高周疲劳区间,疲劳寿命的分散性很大,疲劳极限值可以通过升降法测定,循环基数一般为1e 07次 。
本文忽略了疲劳极限的测定、数据检验和可疑数据取舍,假设试验数据符合正态分布且样本数量充足 。
有这样一组成组法疲劳试验数据,应力比为R=-1,试验环境为室温,如下所示:
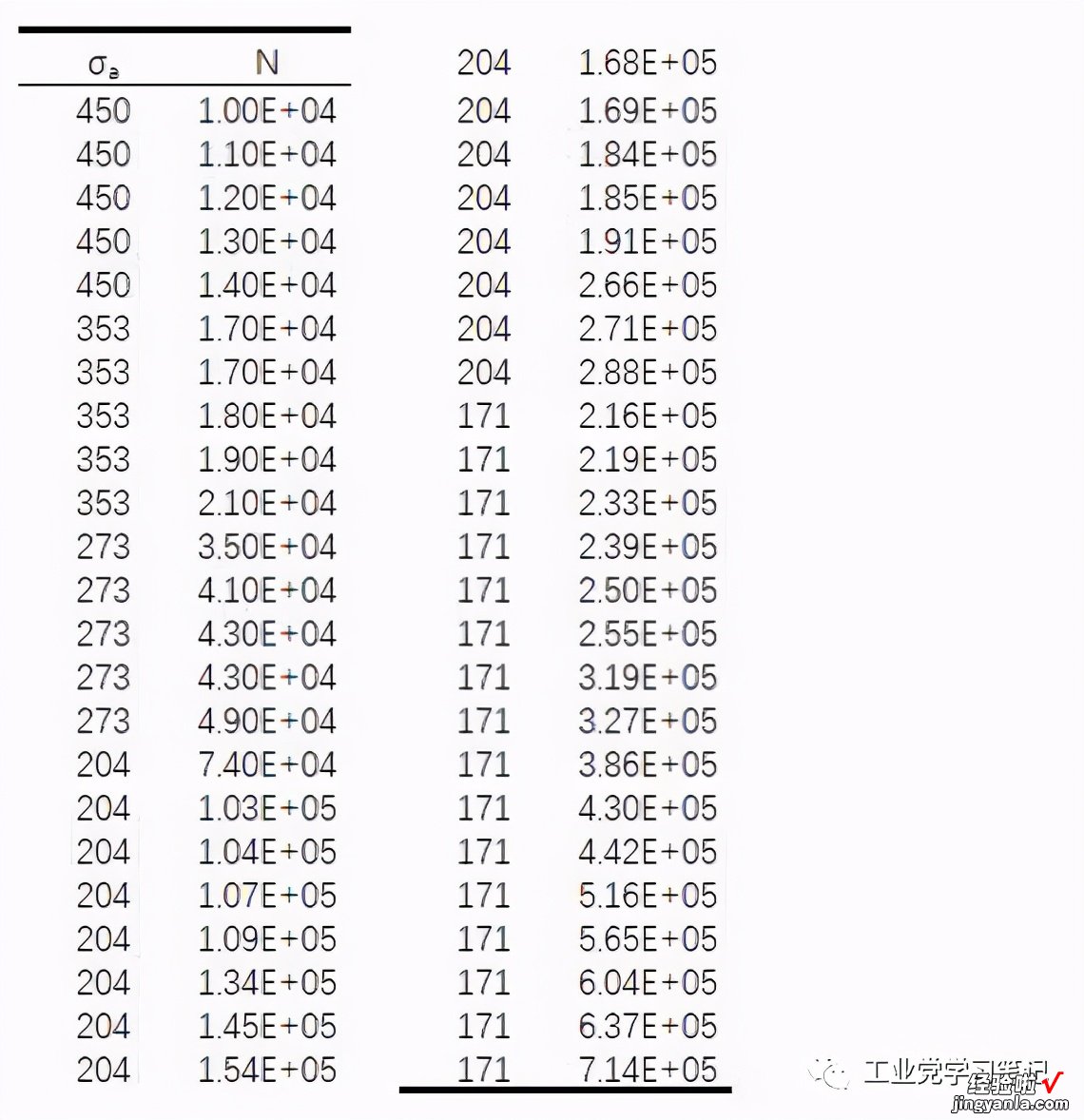
可以假设各个应力水平中,失效寿命呈现正态分布 。将这些数据点绘制于双对数坐标系:
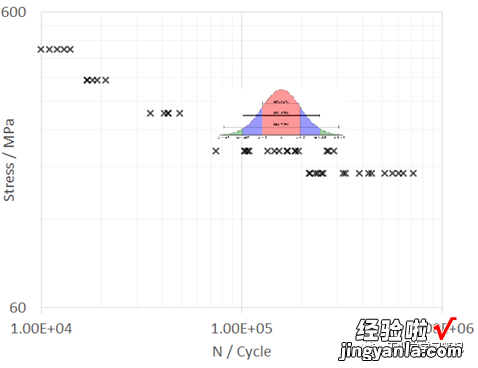
3. 数据处理
3.1 由于材料的S-N特性在双对数坐标系下呈线性,随后将使用最小二乘法对数据进行线性拟合,因此将疲劳数据转换为对数值:

3.2 计算各个应力水平子样的平均值
使用公式:
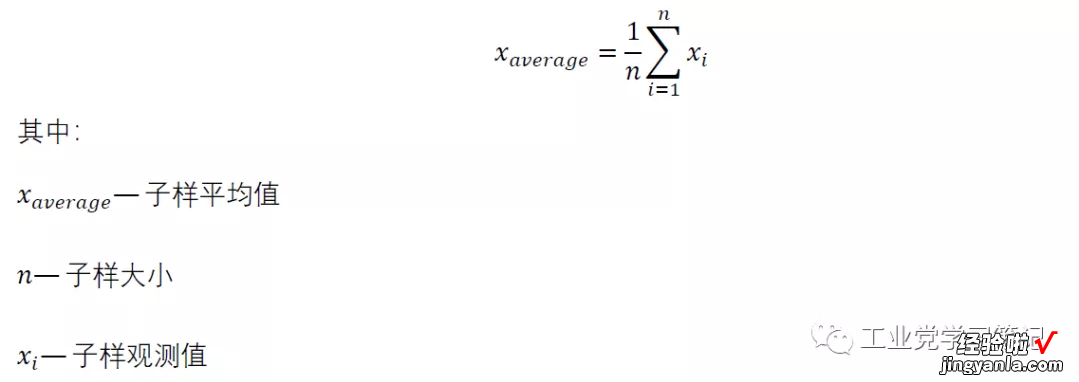
计算结果:
4.0761
x average(σa=353)
4.2634
x average(σa=273)
4.6228
x average(σa=204)
5.1891
x average(σa=171)
5.5633
3.3 计算各个应力水平子样的标准差
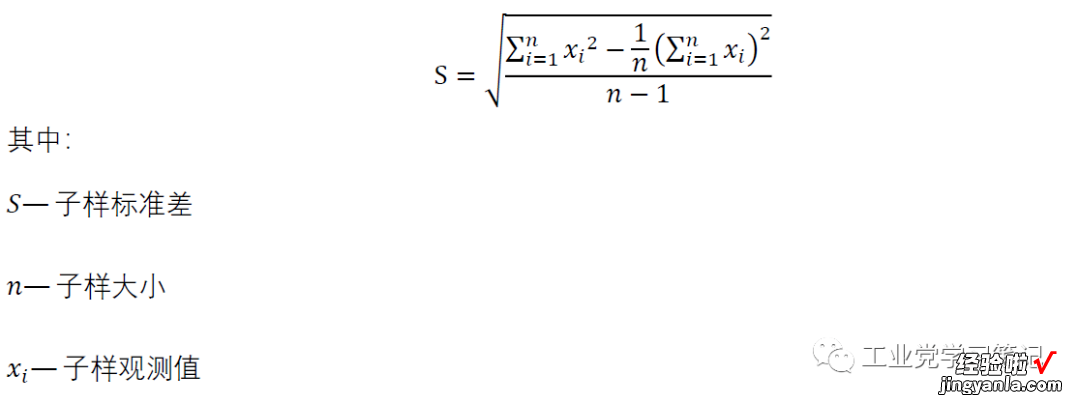
计算结果:
0.0578
S(σa=353)
0.0385
S(σa=273)
0.0526
S(σa=204)
0.1688
S(σa=171)
0.1812
3.4 计算给定存活率P和标准正态偏差Up的概率疲劳寿命xp
概率疲劳寿命的计算公式如下:
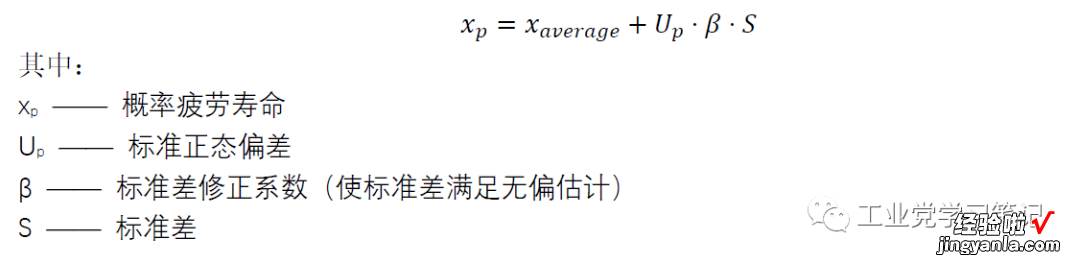
当存活率P=99.9% 时,计算得到:
UP=99.9% = -3.090
β值在标准差修正因数表中查找:
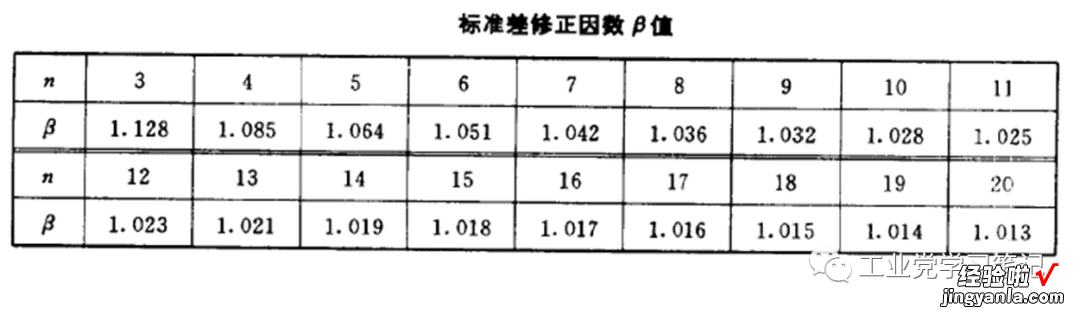
可以计算得到:
3.8862
xp=0.999(σa=353)
4.1368
xp=0.999(σa=273)
4.4498
xp=0.999(σa=204)
4.6586
xp=0.999(σa=171)
4.9939
同理 , 可以计算得到当存活率P=90% 时的概率疲劳寿命:
3.9974
xp=0.9(σa=353)
4.2109
xp=0.9(σa=273)
4.5511
xp=0.9(σa=204)
4.9691
xp=0.9(σa=171)
5.3271
3.5 使用最小二乘法拟合
使用最小二乘法对参数B和A进行估算:
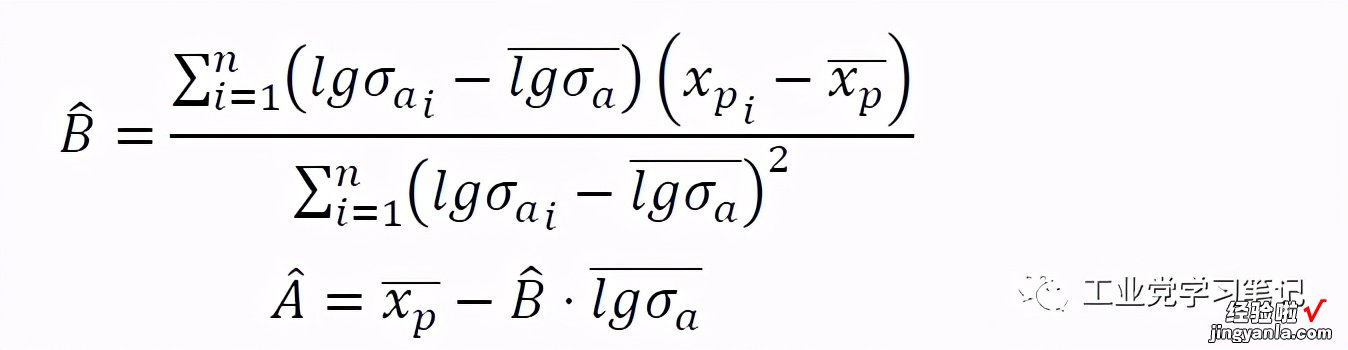
本文采用幂函数拟合P-S-N曲线 。
求得参数B和A后 , 使用如下关系求得疲劳强度指数b和疲劳强度系数S'f :
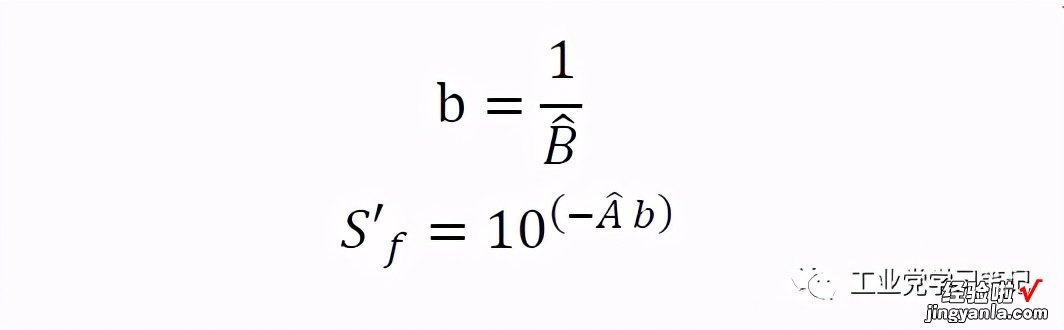
使用上述公式求得如下参数:
1. 存活率为50%时(使用3.2节求得的平均值):
-3.60594
A =
13.52685
b =
-0.27732
S'f =
5639.89
S-N函数表达式:
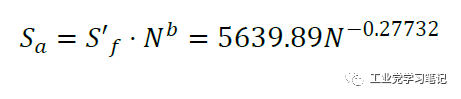
2. 存活率为90%时:
-3.15476
A =
12.29598
b =
-0.31698
S'f =
7899.404
S-N函数表达式:
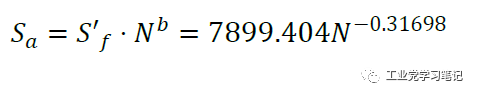
3. 存活率为99.9%时:
-2.518
A =
10.5588
b =
-0.3971
S'f =
15607.4
S-N函数表达式:
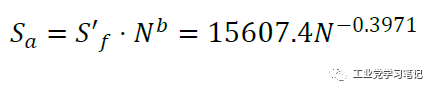
将这3条P-S-N曲线绘制于同一坐标系下:
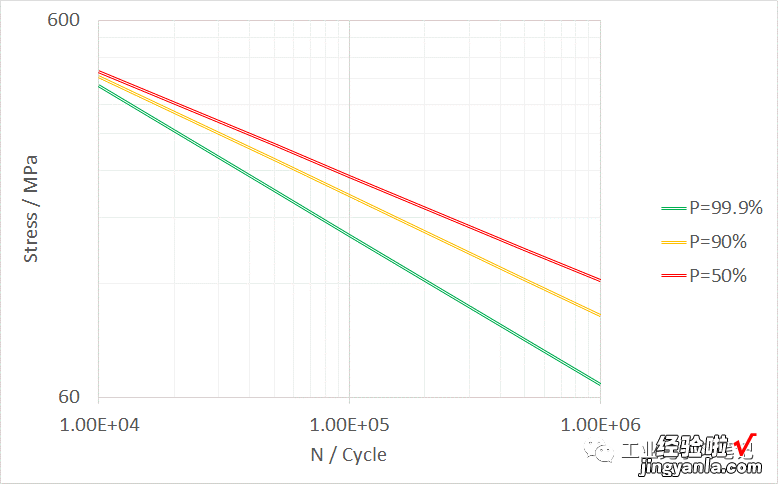
可见 , 存活率越高,S-N曲线的“高度”越低 。
当使用较高的存活率进行疲劳分析时 , 得到的损伤值也会更高 。
将试验数据与P-S-N曲线绘制于同一坐标系下可以更好地显示它们之间的关系:
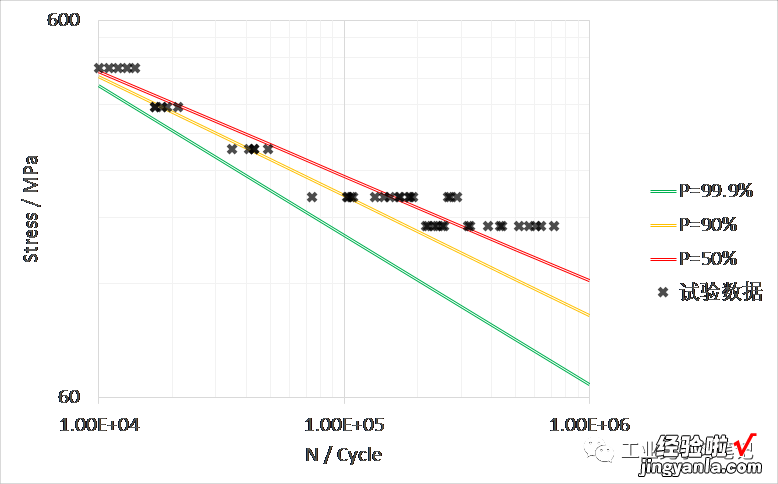
4. 小结
本文简单地描述了P-S-N曲线的制作过程,用制作P-S-N曲线的过程揭示了它的原理 。
在此基础上可以进行如下小节:
1) 材料疲劳的分散性是不可避免的,并且这种分散性随着应力幅的减小而更加显著 。因此在材料疲劳特性的试验分析中必须引入失效概率,否则试验数据无法满足实际工程要求 。
2) 失效概率会显著影响S-N曲线的“高低”,当设计师要求使用不同的存活概率进行CAE疲劳分析时,分析出的损伤值也会受到显著影响 。因此设计师必须慎重选择存活概率 。
参考文献:
[1] 高镇同,疲劳应用统计学 [M]. 北京:国防工业出版社, 1986
[2] Yung-Li Lee,疲劳试验测试分析理论与实践 [M]. 北京:国防工业出版社, 2011
【P-S-N曲线的制作过程】[3] 伊为恺,疲劳试验中的数据处理 [J]. 北京:洪都科技, 1995
