轻松办公-OfficeExcel函数精解
(五十九)
1、VARPA函数
- 函数功能
- 语法
参数说明:
- Value1, value2,... 为对应于样本总体的 1 到 255 个参数 。
- 函数 VARPA 假设其参数为样本总体 。如果数据代表的是总体的一个样本,则必须使用函数 VARA 来计算方差 。
- 参数可以是下列形式:数值;包含数值的名称、数组或引用;数字的文本表示;或者引用中的逻辑值,例如 TRUE 和 FALSE 。
- 逻辑值和直接键入到参数列表中代表数字的文本被计算在内 。
- 包含 TRUE 的参数作为 1 来计算;包含文本或 FALSE 的参数作为 0(零)来计算 。
- 如果参数为数组或引用,则只使用其中的数值 。数组或引用中的空白单元格和文本值将被忽略 。
- 如果参数为错误值或为不能转换为数字的文本 , 将会导致错误 。
- 如果要使计算不包括引用中的逻辑值和代表数字的文本,请使用 VAR 函数 。
- 函数 VARPA 的计算公式如下:
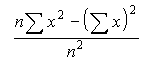
其中 x 是样本平均值 AVERAGE(value1,value2,…) 且 n 是样本大小 。
- 示例
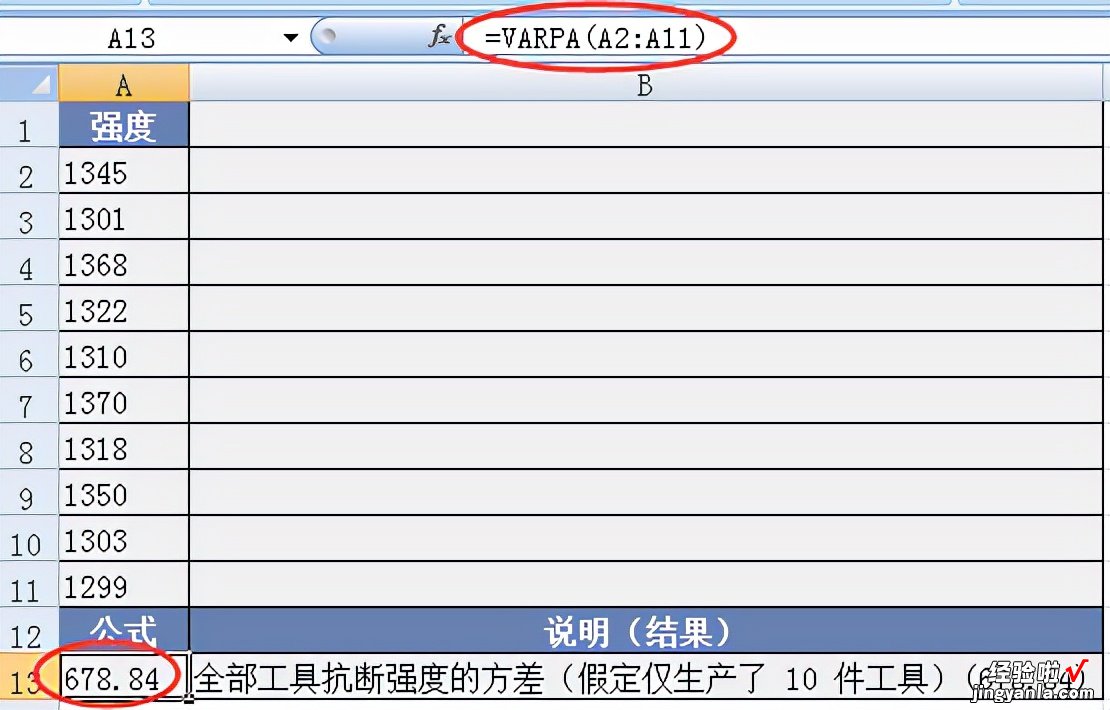
2、WEIBULL函数
- 函数功能
- 语法
参数说明:
- X 参数值 。
- Alpha 分布参数 。
- Beta 分布参数 。
- Cumulative 指明函数的形式 。
- 如果 x、alpha 或 beta 为非数值型,函数 WEIBULL 返回错误值 #VALUE! 。
- 如果 x < 0,函数 WEIBULL 返回错误值 #NUM! 。
- 如果 alpha ≤ 0 或 beta ≤ 0 , 函数 WEIBULL 返回错误值 #NUM! 。
- 韦伯累积分布函数的计算公式如下:
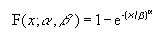
- 韦伯概率密度函数的计算公式如下:
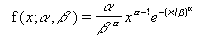
- 当 alpha = 1,函数 WEIBULL 返回指数分布:
- 示例
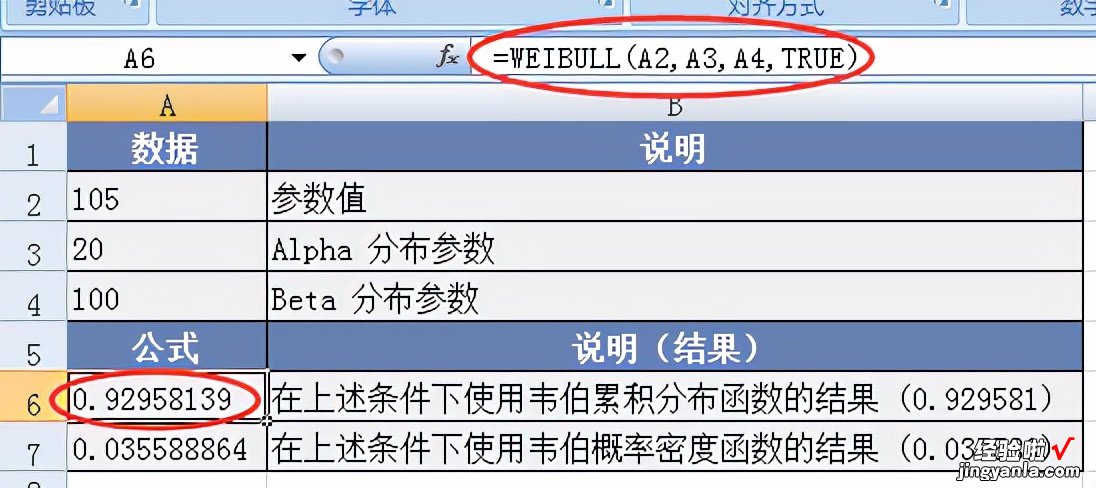

3、ZTEST函数
- 函数功能
若要了解如何在公式中使用 ZTEST 计算双尾概率值的有关信息,请参阅下面的“说明”部分 。
- 语法
参数说明:
- Array 为用来检验 μ0 的数组或数据区域 。
- μ0 为被检验的值 。
- Sigma 为样本总体(已知)的标准偏差 , 如果省略,则使用样本标准偏差 。
- 如果 array 为空,函数 ZTEST 返回错误值 #N/A 。
- 不省略 sigma 时 , 函数 ZTEST 的计算公式如下:
- 省略 sigma 时,函数 ZTEST 的计算公式如下:

其中,x 为样本平均值 AVERAGE(array);s 为样本标准偏差 STDEV(array);n 为样本中的观察值个数 COUNT(array) 。
- ZTEST 表示当基础总体平均值为 μ0 时,样本平均值大于观察值 AVERAGE(array) 的概率 。由于正态分布是对称的,如果 AVERAGE(array) < μ0,则 ZTEST 的返回值将大于 0.5 。
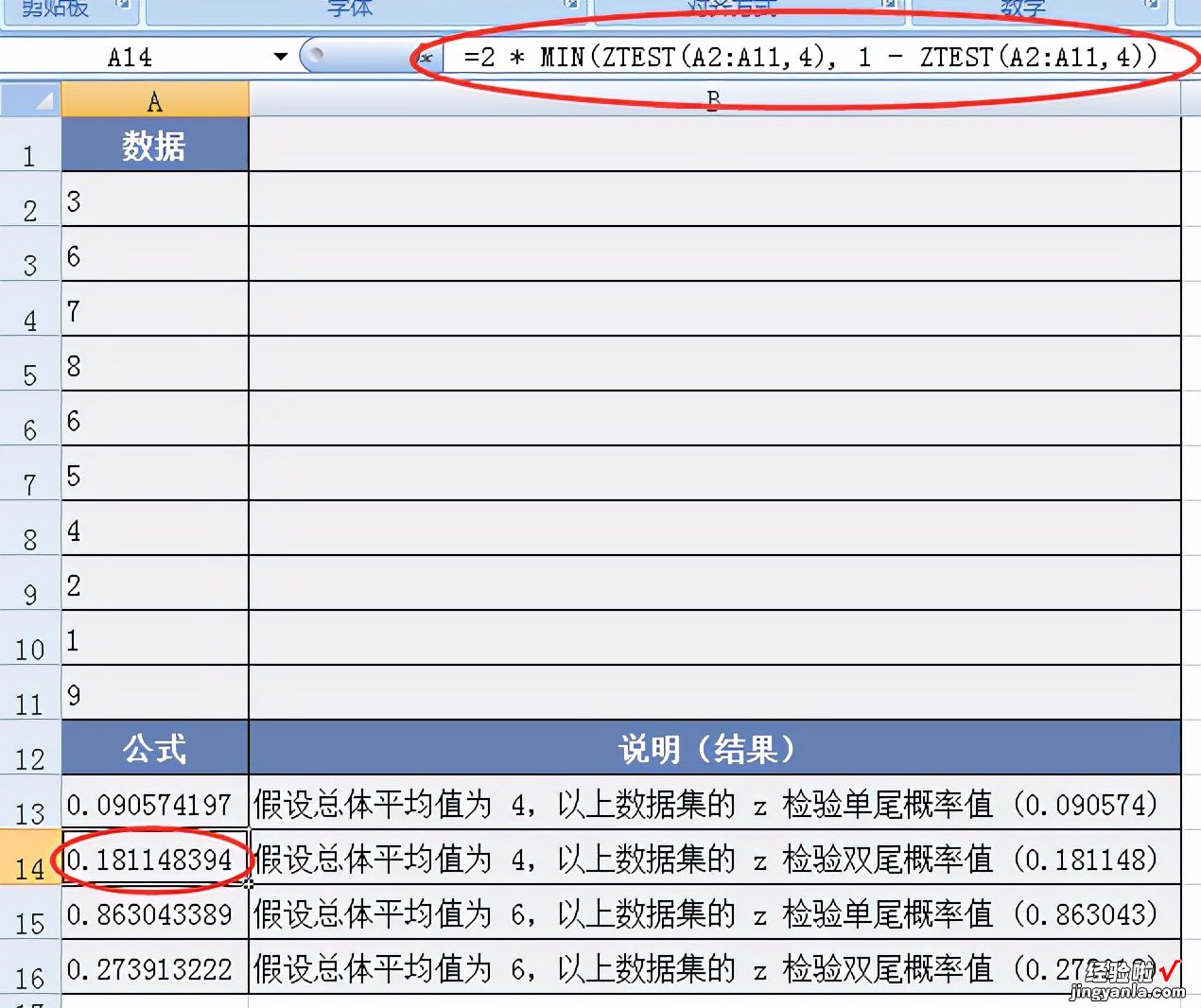
- 当基础总体平均值为 μ0,样本平均值从 μ0(沿任一方向)变化到 AVERAGE(array) 时,下面的 Excel 公式可用于计算双尾概率:
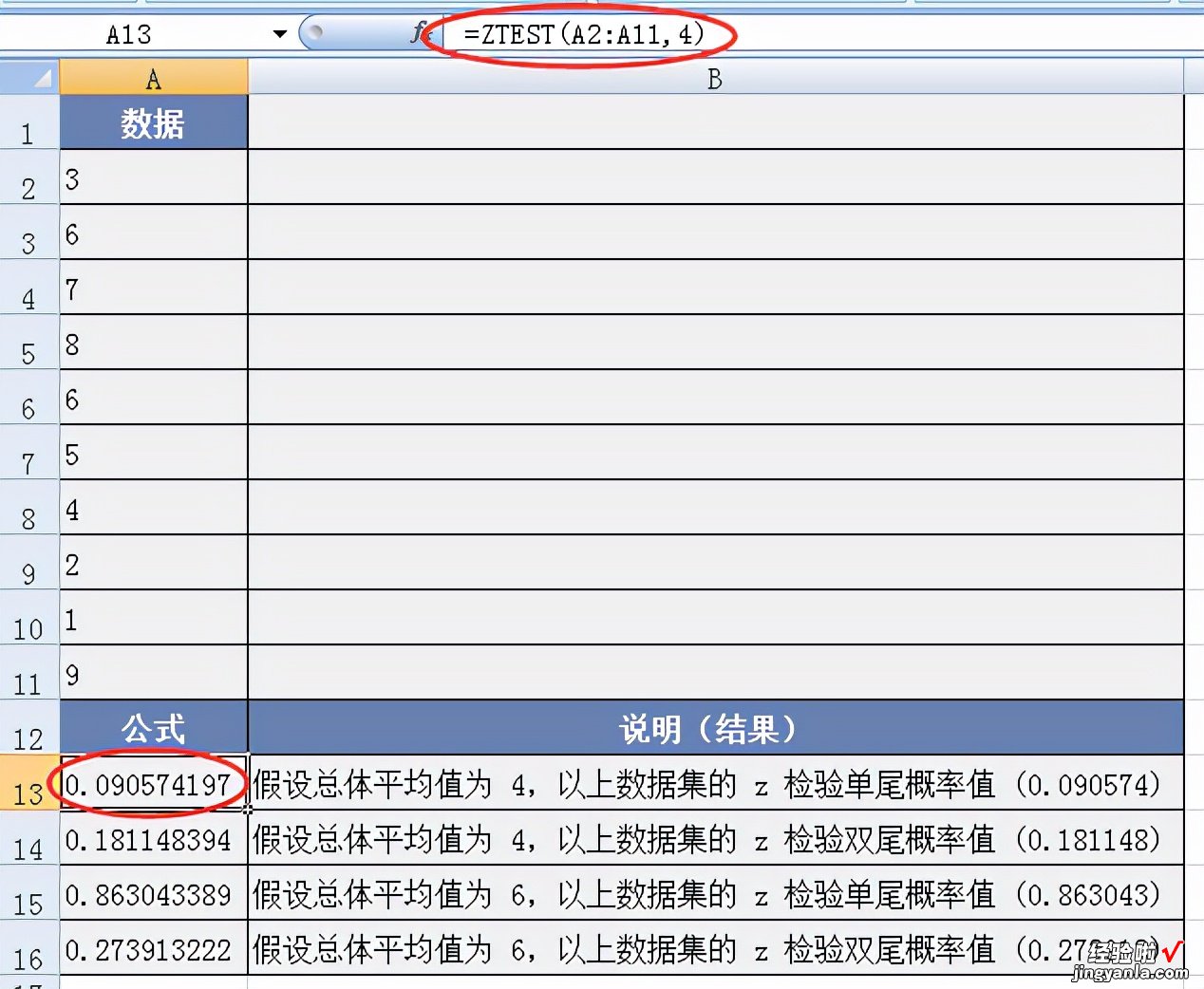
- 示例
【五十九 轻松办公-OfficeExcel函数精解】更多精彩内容将在以后的章节分享给朋友们,请添加好友至收藏 , 欢迎点赞并关注后期内容更新!
