一、复利终值的计算
【案例1】某人将100元存入银行,年利率2%,求5年后的终值?
<解题思路>要通读案例,了解题中给出已知问题 。判断题中已知部分,那些对最终结果起到作用 。
本案例的已知条件是某人现在100万元存入银行 , 利率为2%,最终求的5年后的终值 。通过已知条件可以得到案例要求的是复利终值或也可以这么说是5年后的本利和 。
根据已知条件,回忆一下什么是复利终值和复利终值的计算公式呢?
复利终值是指现在特定资金按照复利计算方法,折算到未来某一时点的价值,或者说现在一定本金在将来一定时间里 , 按复利计算的本金和利息之和 。
本案例的复利终值计算公式:
F=PX(F/P,i,n)
这个公式是如何得到呢?
我们通过一年单利计息进行推导这个公式,已知条件P、i,n , 求P
计算下一年的利息F=PX(1 i)
两年的本利和计算F=PX(1 i)x(1 i)=Px(1 i)
依次类推,随着计息期增加就可以得到如下:
F=PX(1 i)x(1 i)=Px(1 i)﹍﹍﹍Px(1 i)
【通过一次性复利终值和现值的案例,剖析复利现值和终值的基本计算】即可以得到:F=Px(1 i)

(1 i)是复利终值系数,用符号表示PX(F/P,i,n),其中P称为现值或称为初始值 , F为终值或称为本利和,i是年利率,n是计息期 。即 , 复利终值系数可以表示为F=PX(F/P,i,n),通过符号(F/P,i,n)书写可以看出来,P、i、n的值都是已知的,而F是未知 。在书写上未知放在已知前面 , 便于确定公式正确书写 。
-
按照已知条件我们可以得到这样已知条件 , 即P=100 , i=2%,n=5 。但是关键这里的(F/P,i,n)的值怎么计算出来呢?通过复利终值系数表就可以查到终值的数据 。如图:
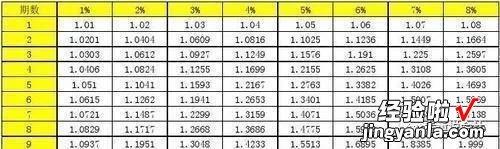
复利终值系数表怎么使用呢?
复利终值系数表的竖列代表是计息期,行代表的利率 。在行与竖列交汇处就是终值系数 。那么本案例的(F/P,2% , 5)的值是多少 。查表可知应是(F/P,2%,5)=1.1041
本案例答案应是:F=PX(F/P,i,n)=100X(F/P,2%,5)=100X1.1041=110.41 二、 二、一次性复利现值计算
【案例2】某人为了5年后能从银行取出100元 , 在年利率2%的情况下,求当前应存入多少元 。
<解析>通读案例可以得到以下已知条件:
F=100 , i-=2%,n=5.求P得值 。
现在我们并不知道复利现值的公式 , 但是却知道复利终值的公式 。
复利终值的公式:F=Px(1 i)
将复利终值公式移项可得到P=F÷(1 i),
进一步简化可得:P=FX(1 i)﹣
(1 i)﹣是复利现值系数,即用符号表示为(P/F , i,n) , 就可得到如下公式:
P=FX(P/F,i , n)
本案例的答案是P=FX(P/F,i,n)=100X(P/F,2%,5)=90.57
通过案例我们可以得出这样一个结论:
复利现值是指未来的某一时点的特定资金按复利计算方法,折算到现在的值 , 或者说是为了将来取得一定本利和,现在所需要的本金 。
三、复利现值与终值的关系
通过复利现值系数(1 i)﹣?与复利终值系数(1 i)可以看出复利现值与复利终值的系数是互为倒数 。复利终值与复利现值互为逆运算 。
