数学的回归分析
回归分析是数学的一种统计分析方法,基于x、y轴的数据,在二维坐标系中寻找直线性的拟合方程,并分析散点与回归直线的偏离误差 。这是最简单的直线性的回归分析 。在数据散点图具有相对的集中、直线性特征的前提下,通常会采取这种拟合方式,以达到简化分析的目的 。
而线性拟合的方法更丰富一些,且可以拟合曲线,这种曲线的拟合方程,有利于方便插值的补充 。而回归分析,更近似这种曲线线性拟合的简单近似值或者局部 。
曲线拟合方程并不一定具有预测功能,以往的文章分析过 。对于决定性系统 , 曲线拟合可存在预测意义;而对于随机系统、混沌系统,曲线拟合并不一定具有预测意义 , 甚至就没有预测意义 。
【回归分析与线性拟合、时序分析、sinx的分形迭代、太极思想的关联】回归分析整体给人的感觉就是数据好似具有回归主拟合线的特征 。回归分析的一种通常是动态的时序性的数据,这部分与时序性分析有关 。而时序性分析是动态的分析 。
时序性的回归(动态的回归)
能够最简化、最简单表达时序性线性回归的是正弦曲线 。它既可以静态表达,又可以动态表达 。古人的太极图中,包含着这种时序性回归思想的数理 。
对于简单的直线性的回归,复杂化的结果就是回归线是曲线的 。而sinx是最简化表达的一种特殊性 。曲线拟合则是复杂的,由系统本身的特性决定是否具有回归性 。
sinx的分形迭代
(注:以下部分内容数学书中没有 。)sinx的分形:
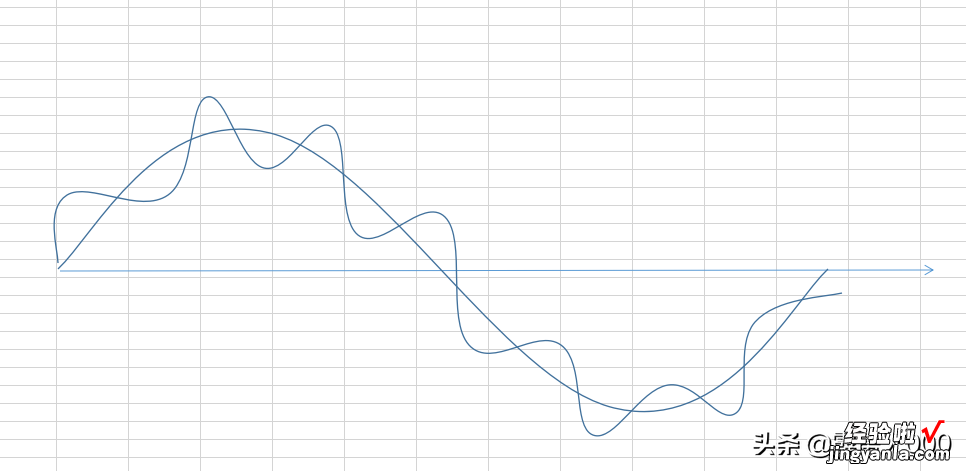
sinx的分形
sinx的分形迭代

sinx的分形迭代
以上是示意图 , 并不数学性的标准 。仅仅说明这种分形的特征 。我们可以利用傅立叶函数分级来准确地画这种简单的sinx迭代分形 。
葛兰碧均线类似这种简单的sinx分形,但仅仅表达了其中的一种理想化的分形 。因为细节的分形即便最简化分类也可以基于1/2或者1/3或1/8、1/9进行分形,几何细节以及整体特征并不同 。
这种sinx分形迭代的数学特征
1、具有动态时序性回归的特征,但回归线不是直线,而是特定的sinx曲线 。2、具有明显的分形迭代特征 。也就是整体系统存在一定的决定性,也可陷入混沌系统 。笔者基于简化,利用分叉理论,对于最简单的1/2分形迭代系统,先假定在3.6分数维陷入混沌 。实际数字可能有差异 。
