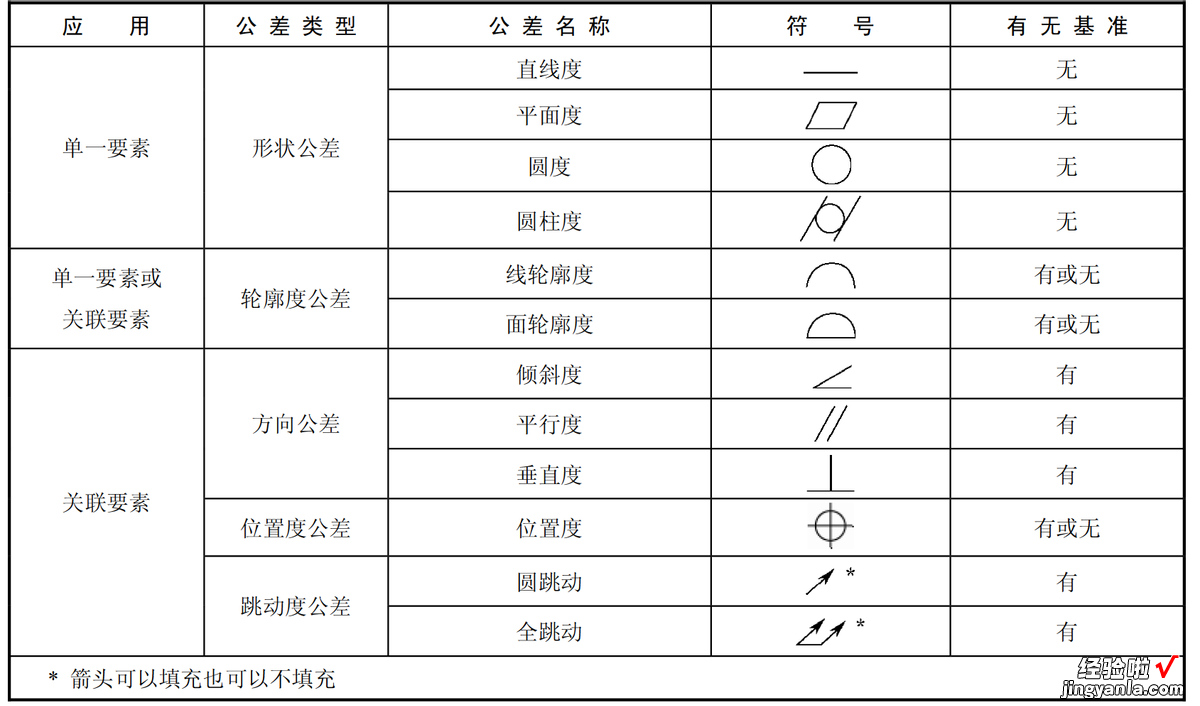
表 1?1几何公差12个符号及其分类
1.形状公差
形状公差有4个符号,即直线度、平面度、圆度和圆柱度 。因为形状公差只是管控自己的形状误差,所以形状公差图纸标注不需要带基准 。
2.轮廓度公差
轮廓度公差有2个符号,即线轮廓度和面轮廓度 。轮廓度公差图纸标注可以带基准,也可以不带基准(管控形状、相对位置、尺寸大小等) 。
3.方向公差
方向公差有3个符号,即倾斜度、平行度和垂直度 。方向公差图纸标注必须有基准 。
4.位置度公差
位置度公差图纸标注可以带基准,也可以不带基准(管控相对位置) 。
5.跳动度公差
跳动度公差有2个符号,即圆跳动和全跳动 。跳动度公差图纸标注必须带基准 。
24个修饰符号
这里仅仅举几个例子进行解释 。
表 1?2 常见的修饰符号
1.最大实体状态(MMC)和最大实体边界(MMB)
最大实体符号标注示例如图1?29所示 。最大实体符号可以标注在公差后面 , 也可以标注在基准后面,标注在公差后面叫作最大实体状态(MMC) , 标注在基准后面叫作最大实体边界(MMB) 。

图 1?29最大实体符号标注示例
2.最小实体状态(LMC)和最小实体边界(LMB)
最小实体符号标注示例如图1?30所示 。最小实体符号可以标注在公差后面,也可以标注在基准后面,标注在公差后面叫作最小实体状态(LMC),标注在基准后面叫作最小实体边界(LMB) 。

图 1?30最小实体符号标注示例
3.独立(Independency)
独立符号只能标注在尺寸公差后面,表示公差原则采用独立原则 。
4.统计公差(StatisticalTolerance)
统计公差符号标注示例如图1?31所示,统计公差符号ST可以标注在尺寸公差和几何公差后面 。标注统计公差符号后,应该在图纸中加上注释“标注统计公差符号的要素,生产加工时必须用统计过程管控” 。
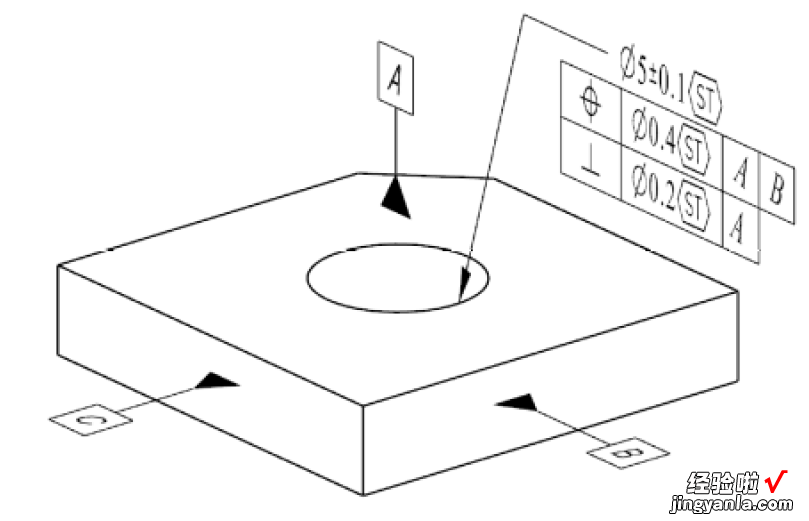
图 1?31统计公差符号标注示例
5.连续要素(ContinuousFeature)
连续要素是指把两个或多个断开的要素 , 或者断开的规则尺寸要素,当作单个要素或单个规则的尺寸要素处理 。连续要素符号CF可以应用标注在以下3种情况 。
(1)标注在规则尺寸要素的尺寸公差后面 。
(2)标注在几何公差附近,几何公差应用在被断开的表面要素 。
(3)标注在基准要素符号附近,基准要素符号应用在被断开的要素 。
连续要素符号标注示例(一)如图1?32所示,连续要素符号应用在被断开的3个规则尺寸要素轴的尺寸公差上,表示要把3个断开的规则尺寸要素当作单个规则尺寸要素处理 。
连续要素符号标注示例(二)如图1?34所示,连续要素符号应用在基准要素符号A上,表示把6个断开的平面要素当作单个大平面要素,然后作为基准要素A 。相当于6个平面没有断开,当作一个整体考虑 。
连续要素符号标注示例(三)如图1?33所示,连续要素符号应用在轮廓度公差框格附近 , 表示被断开的6个表面当作单一的表面,在轮廓度0.4的公差带里 。这相当于6个表面没有断开,当作一个大表面整体进行管控 。
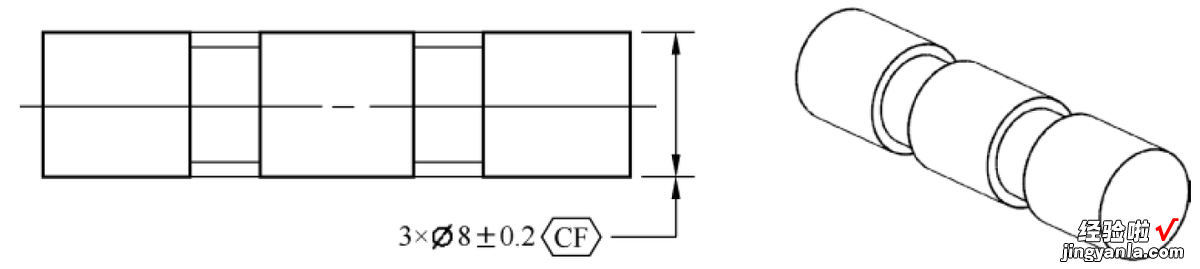
图 1?32连续要素符号标注示例(一)
图 1?33连续要素符号标注示例(三)
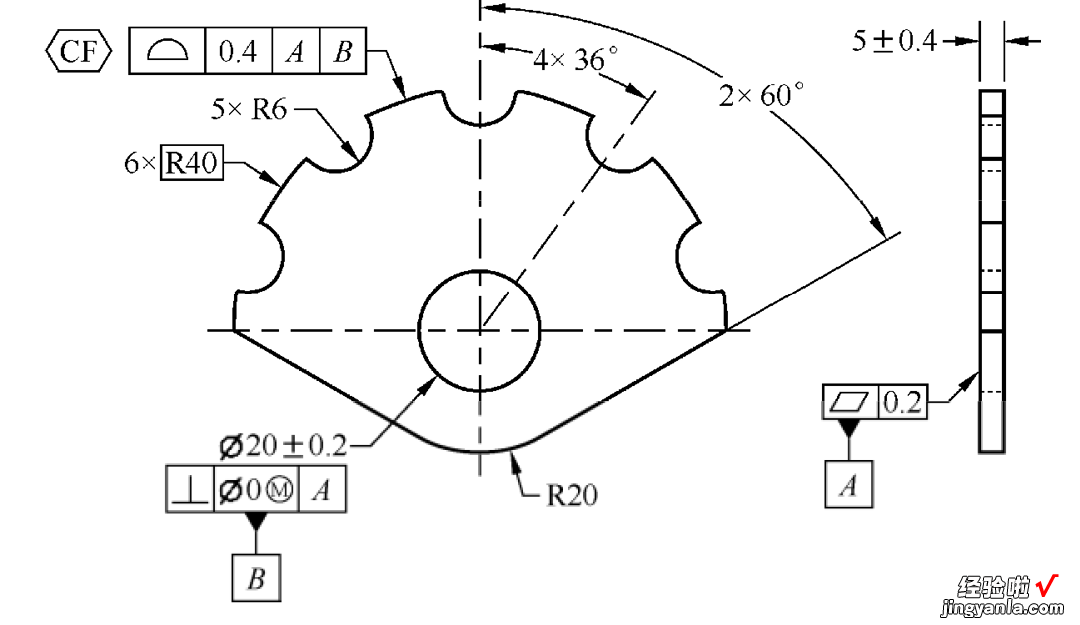
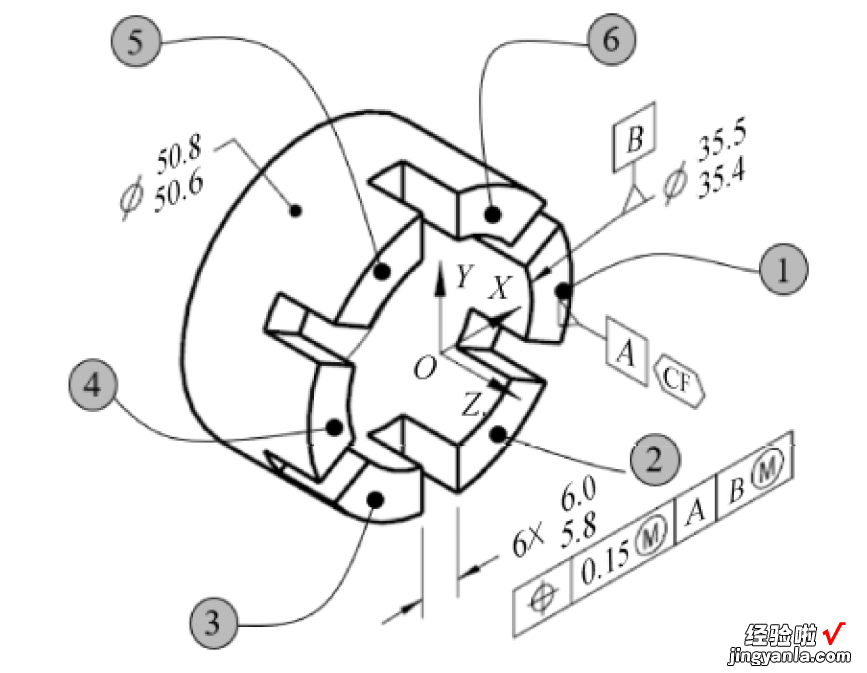
图 1?34连续要素符号标注示例(二)
6.直径(Diameter)
直径符号标注示例如图1?35所示,直径符号?可以标注在尺寸公差前面,管控孔、轴的直径大小 。直径符号?标注在几何公差前面,表示公差带的形状是圆柱 。
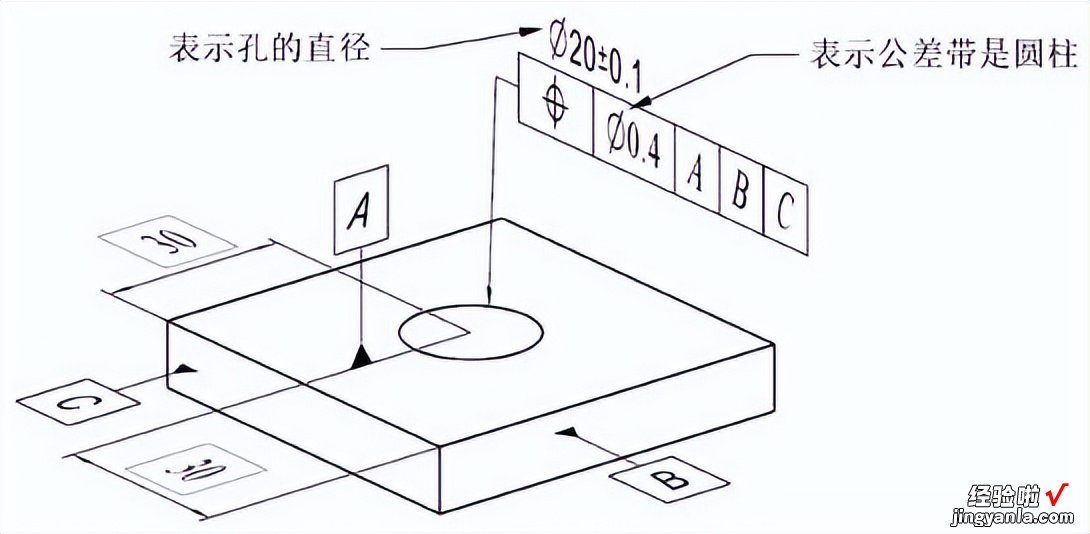
图 1?35直径符号标注示例
7.方形(Square)
方形符号标注示例如图3-14所示,方形符号□标注在尺寸前,用来定义一个正方形尺寸 。
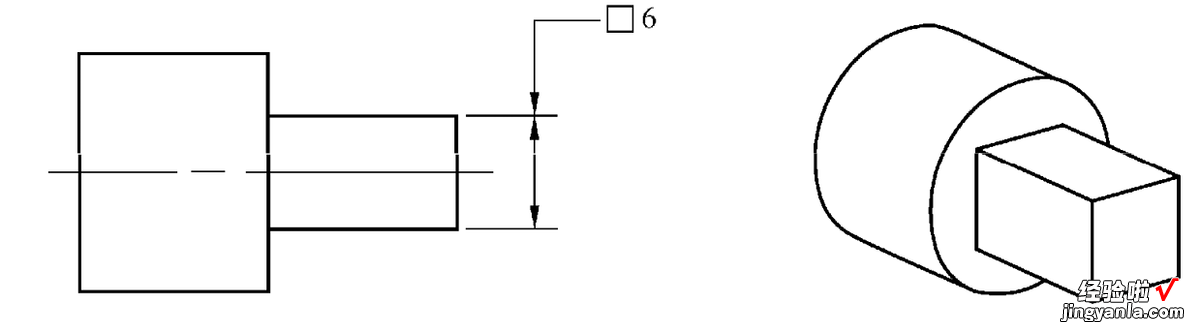
图 1?36方形符号标注示例
公差原则
公差原则与相关要求实际就是解释了尺寸公差与几何公差之间的关系,GD&T公差原则与相关要求示例如图1?37所示 。主要包括基本公差原则和相关要求:基本公差原则包括包容原则(Rule#1)、独立原则和与要素尺寸无关原则(Rule#2);相关要求包括最大实体要求、最小实体要求和尺寸基本规则 。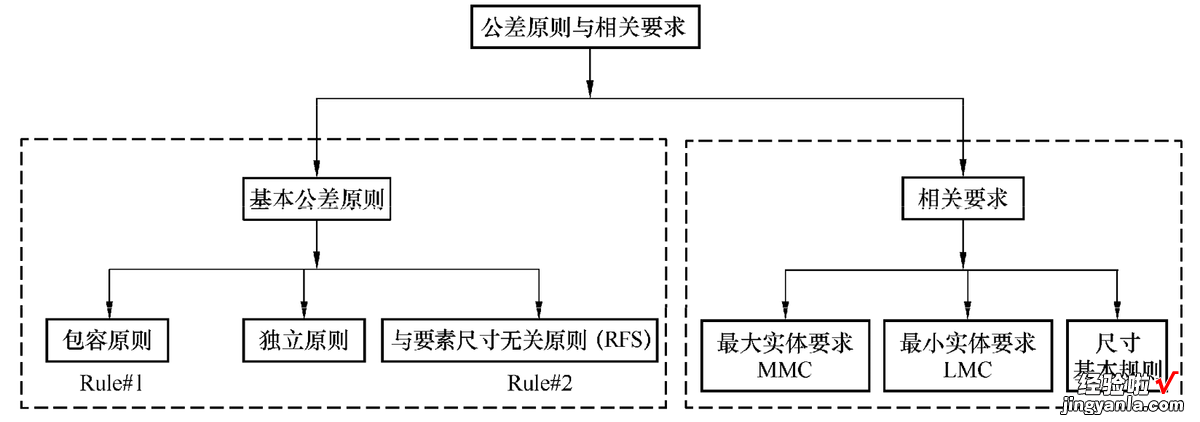
图 1?37公差原则与相关要求示例
包容原则
包容原则解释了尺寸公差和形状公差之间的关系,指的是单个规则的尺寸要素的形状误差被标注的尺寸公差管控,具体要求如下 。(1)规则尺寸要素的表面不能超过最大实体包容边界 。
(2)当规则尺寸要素的局部实际尺寸处处等于最大实体(MMC)尺寸时,不允许有形状误差 。当局部实际尺寸偏离最大实体时,允许有局部的形状误差,其值就等于实际局部尺寸与最大实体尺寸的差值 。
(3)当规则尺寸要素加工在最小实体时,允许有最大的形状误差 。
(4)当应用几何公差,要求规则尺寸要素在最小实体时形状理想,那么规则尺寸要素不需要要求在最大实体形状理想 。
(5)包容原则只适用于单个的规则尺寸要素 。
包容原则确保了单个规则的尺寸要素的装配,如孔轴配合 。当包容原则应用在外部尺寸要素时,如轴,其最大实体包容边界等于其最大极限尺寸(即轴的最大实体尺寸) 。
当包容原则应用在内部尺寸要素时,如孔,其最大实体包容边界等于最小极限尺寸(即孔的最大实体尺寸) 。
包容原则应用在外部尺寸要素 , 如轴,当轴的直径在最大实体(即最大极限尺寸)时,轴的形状(包括直线度、圆度和圆柱度)必须理想;当轴的实际直径小于最大极限尺寸(即最大实体尺寸)时,允许轴有相应的形状误差,其形状误差的大小等于实际轴的直径尺寸与最大极限尺寸(即最大实体尺寸)的差值 。轴的尺寸和形状公差的关系标注示例如图1?38所示 。
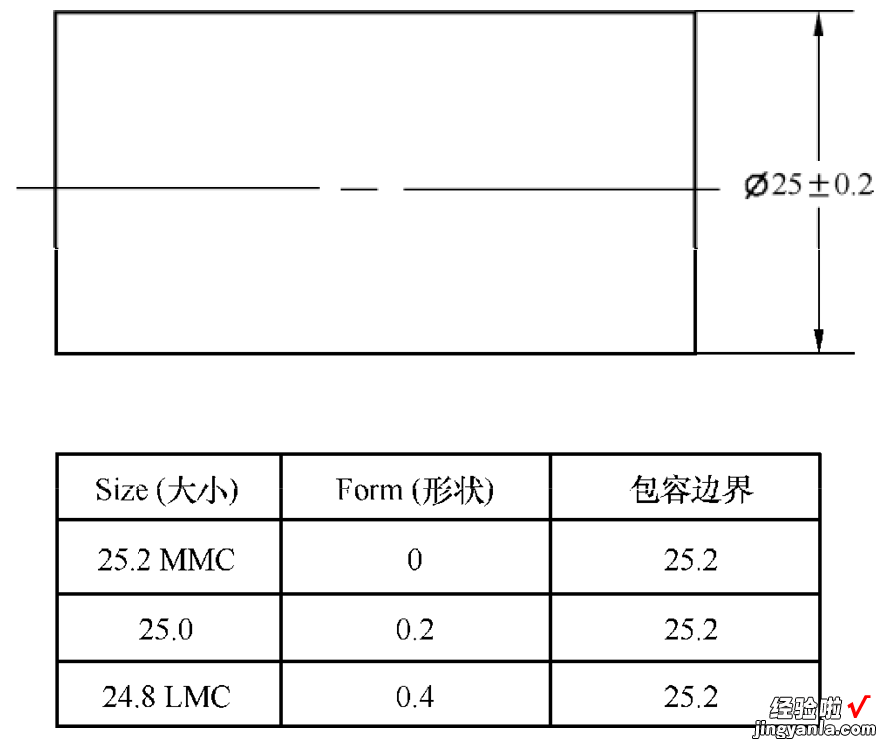
图 1?38轴的尺寸和形状公差的关系标注示例
包容原则应用在内部尺寸要素,如孔,当孔的直径在最大实体(即最小极限尺寸)时,孔的形状(包括直线度、圆度和圆柱度)必须理想;当孔的实际直径大于最小极限尺寸(即最大实体尺寸)时,允许孔有相应的形状误差,其形状误差的大小等于实际孔的直径与最小极限尺寸(即最大实体尺寸)的差值 。孔的尺寸大小和形状公差的关系标注示例如图1?39所示 。
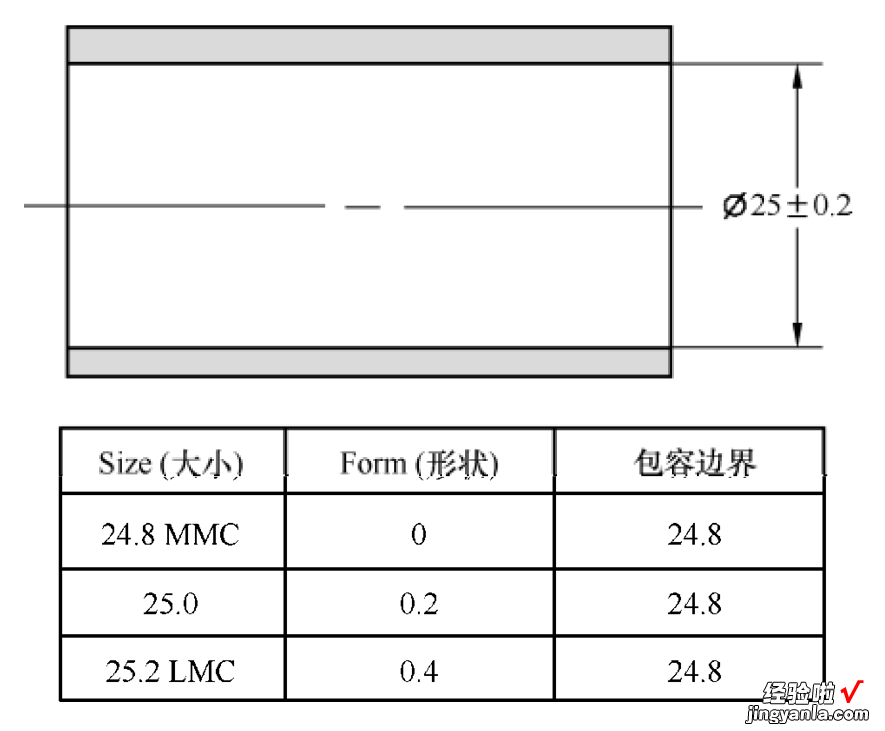
图 1?39孔的尺寸大小和形状公差的关系标注示例
包容原则的特点:
(1)被测要素的实际轮廓在给定长度上处处不应超过最大实体包容边界,即实际要素的配合作用尺寸不得超出最大实体尺寸 。
(2)当要素的局部实际尺寸处处为最大实体尺寸时,必须有理想形状,不允许有任何形状误差 。
(3)当要素的局部实际尺寸偏离最大实体尺寸时,允许局部的形状误差 。其偏离量可补偿给形状误差,即形状误差等于偏离量 。
(4)当实际要素处于最小实体状态时,允许的形状误差达到最大值 。
(5)要素的局部实际尺寸不得超出尺寸公差范围 。
(6)尺寸公差不仅限制了要素的实际尺寸,还控制了要素的形状误差 。
(7)在包容原则下,表面形状公差不会超过尺寸公差 。
包容原则的应用:
包容原则一般应用于孔轴配合 , 保证配合性质 。特别是配合公差较小时,如最小间隙或最大过盈的精密配合 。要想保证孔轴配合有一定的间隙量和过盈量,孔和轴的实际配合表面都不能超过自己的最大实体包容边界 。包容原则很好地保证了这一功能要求 。包容原则应用之孔轴配合标注示例如图1?40所示,孔和轴的最大实体尺寸都是30,在包容原则规定下,孔和轴的实际表面都不会超过自己的最大实体包容边界尺寸30,从而保证了标注所示的公差配合功能 。
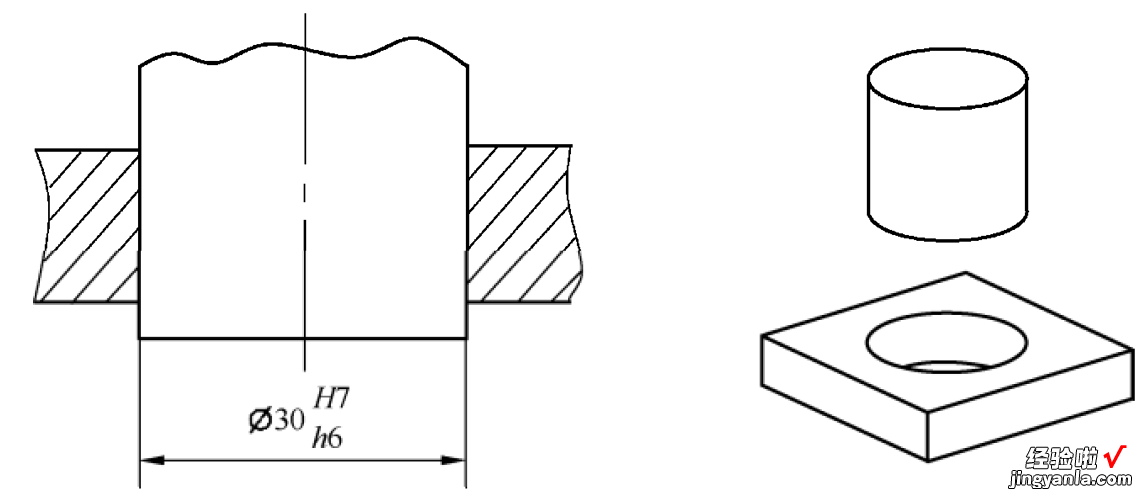
图 1?40包容原则应用之孔轴配合标注示例
包容原则的边界:
包容原则应用于规则尺寸要素,其包容原则边界与规则尺寸要素的理想几何形状一样 。常见的包容原则的边界如下 。
(1)圆柱面,如包容原则应用于圆孔或圆轴 。
(2)两个平行平面,如包容原则应用于槽或板(两相互平行面的尺寸要素) 。
(3)一个球面,如包容原则应用于球 。
最大实体包容边界应用于尺寸要素的整个长度、宽度、深度,包容原则通过确保局部表面不会超过最大实体MMC的理想边界,从而保证了配合功能 。
包容原则与规则尺寸要素的关系:
1.包容原则与单个规则尺寸要素
包容原则只控制单个规则尺寸要素的形状公差,不管控规则尺寸要素的方向和位置公差,规则尺寸要素的垂直度,对称度、位置度必须用相应的方向和位置公差管控 。
包容原则中尺寸公差只管控形状公差图纸标注示例(孔),如图1?41所示 , 尺寸公差?10±0.2和尺寸公差?8±0.2只管控两个孔的形状公差,即孔的圆柱度、圆度或直线度 。
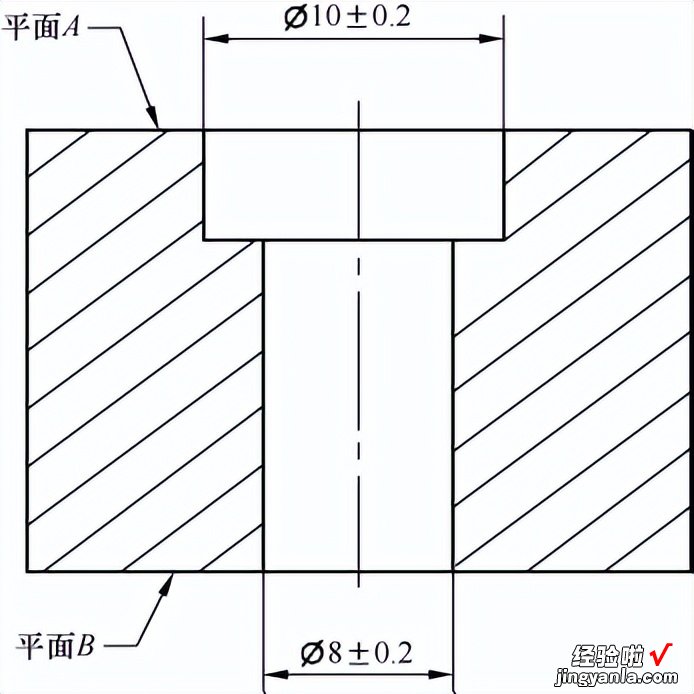
图 1?41包容原则中尺寸公差只管控形状公差图纸标注示例(孔)
不能管控两个孔的同轴度关系,以及每个孔平面A和平面B的垂直度公差 。
包容原则中尺寸公差只管控形状公差图纸标注示例(轴),如图1?42所示,两个直径尺寸为10的轴,理想状态同轴 。由包容原则可知,轴1和轴2都有一个最大实体包容边界 , 其尺寸等于最大实体尺寸,轴的实际外表面不能超过自己的最大实体包容边界 。当轴的实际直径尺寸小于最大实体尺寸时,允许有相应的形状误差,最大形状误差不会超过自己的尺寸公差 。所以包容原则管控了轴1和轴2的形状误差,但轴1和轴2的最大实体包容边界是独立的,两个包容边界不需要保持相互的位置(同轴)和方向(平行)关系 , 如图1?42所示,轴1和轴2的同轴度关系没有被管控 。
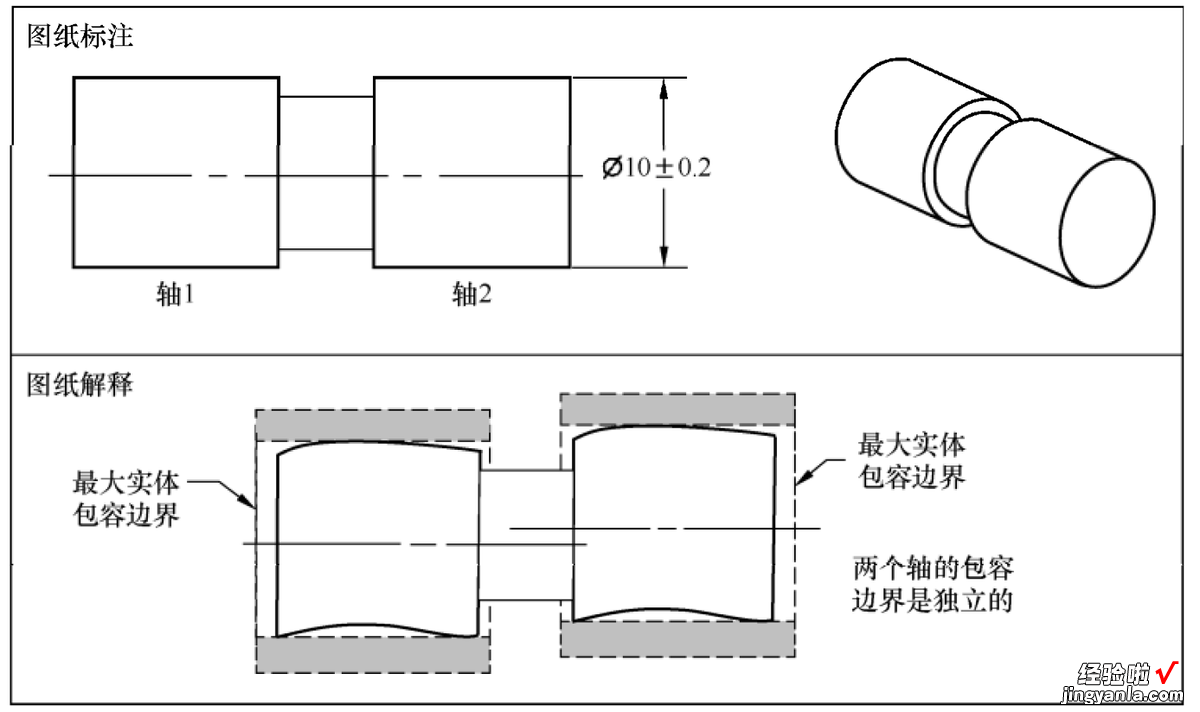
图 1?42包容原则中尺寸公差只管控形状公差图纸标注示例(轴)
2.连续要素(CF)与包容原则
连续要素(CF)与包容原则图纸标注示例如图1?43所示,两个直径尺寸为10的轴 , 理想状态是同轴,图纸标注在尺寸公差后面加了连续要素符号(CF) 。由连续要素符号的定义可知,左右两个轴应该当作一个连续的轴整体管控,在包容原则下,就要用一个尺寸为10.2的最大实体包容边界同时把两个轴包在里面,两个轴的实际外表面不能超出最大实体包容边界 。当两个轴的实际横截面尺寸处处都等于最大实体尺寸10.2时,两个轴不仅要求自身的形状理想,而且相互位置也要理想,不允许有同轴误差 。当其中一个轴的非关联实际包容配合面尺寸小于最大实体包容边界尺寸10.2时,就允许两个轴有同轴度误差即相互位置误差 , 其值就等于轴的非关联实际包容配合面的尺寸与最大实体包容边界尺寸的差值 。综上所述,规则尺寸要素加上连续要素符号(CF),在包容原则下就可以管控几个连续的规则尺寸要素的相互位置关系了 。
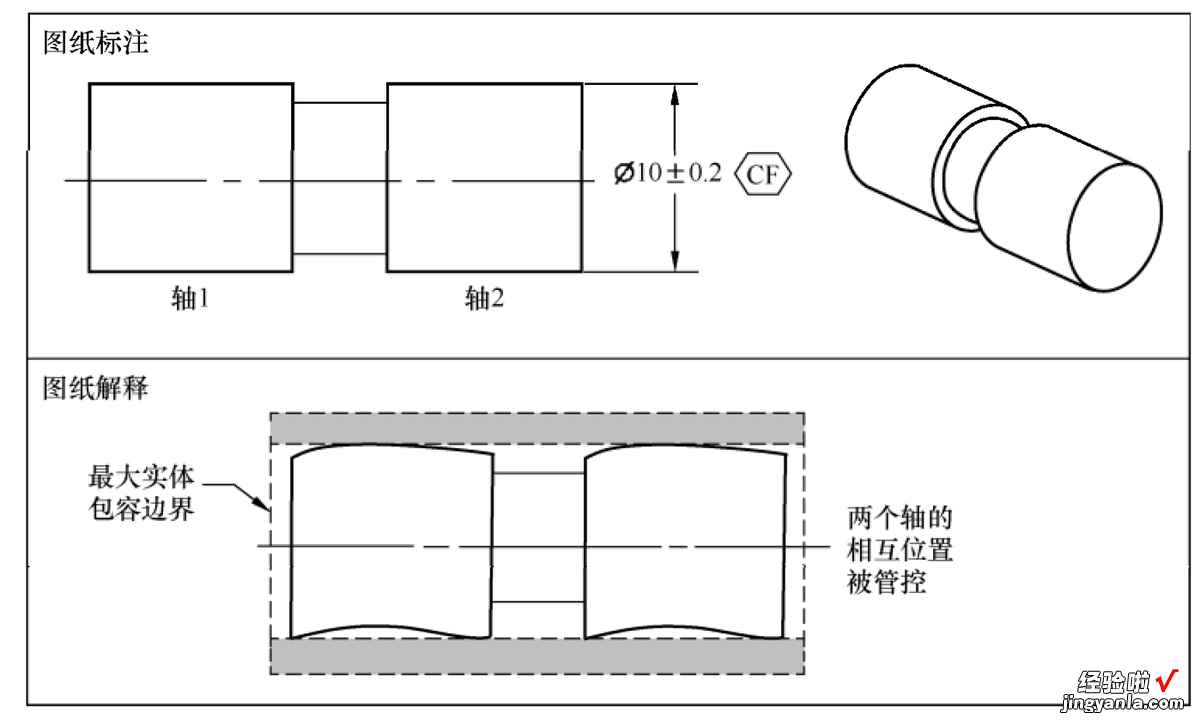
图 1?43连续要素(CF)与包容原则图纸标注示例
包容原则的检测
包容原则中有两个重要的尺寸需要检测 。
(1)检测零件的非关联实际包容配合面,其尺寸要小于或等于、大于或等于最大实体包容边界尺寸,以保证装配性能 。对于外部规则尺寸要素(如轴),非关联实际包容配合面就是最小外接圆柱面,其值小于或等于最大实体包容边界尺寸 。对于内部规则尺寸要素(如孔),非关联实际包容配合面就是孔的最大内切圆柱面,其值大于或等于最大实体包容边界尺寸 。
(2)检测零件的任意一个横截面实际局部两点尺寸不要超出尺寸公差范围,以保证尺寸大小不超差 。在测两点尺寸时,选取的横截面要垂直于非关联实际包容配合面的轴线 。
轴的包容原则检测标注示例如图1?44所示 , 图中轴的非关联实际包容配合面的尺寸D要小于或等于最大实体包容边界尺寸10.1,实际局部截面两点尺寸d1~d3要在尺寸公差?10±0.1范围内 。
工程中检测包容原则最常用的方法是通止规法,通规测量零件非关联实际包容配合面尺寸要小于或等于最大实体包容边界,止规测量零件实际局部尺寸不能超过尺寸公差范围 。对于图4-8中的轴,其包容原则检测之通止规法标注示例如图1?45所示 。通规测量就是做一个直径尺寸等于轴的最大实体尺寸10.1的套筒,只要实际轴能够顺利通过通规套筒,就说明轴的实际外表面没有超过最大实体包容边界10.1 。用卡规(止规)测量轴的实际局部尺寸,只要卡规在轴的任意一个横截面能够止住 , 就说明轴的实际局部截面尺寸不会超过尺寸公差范围 。
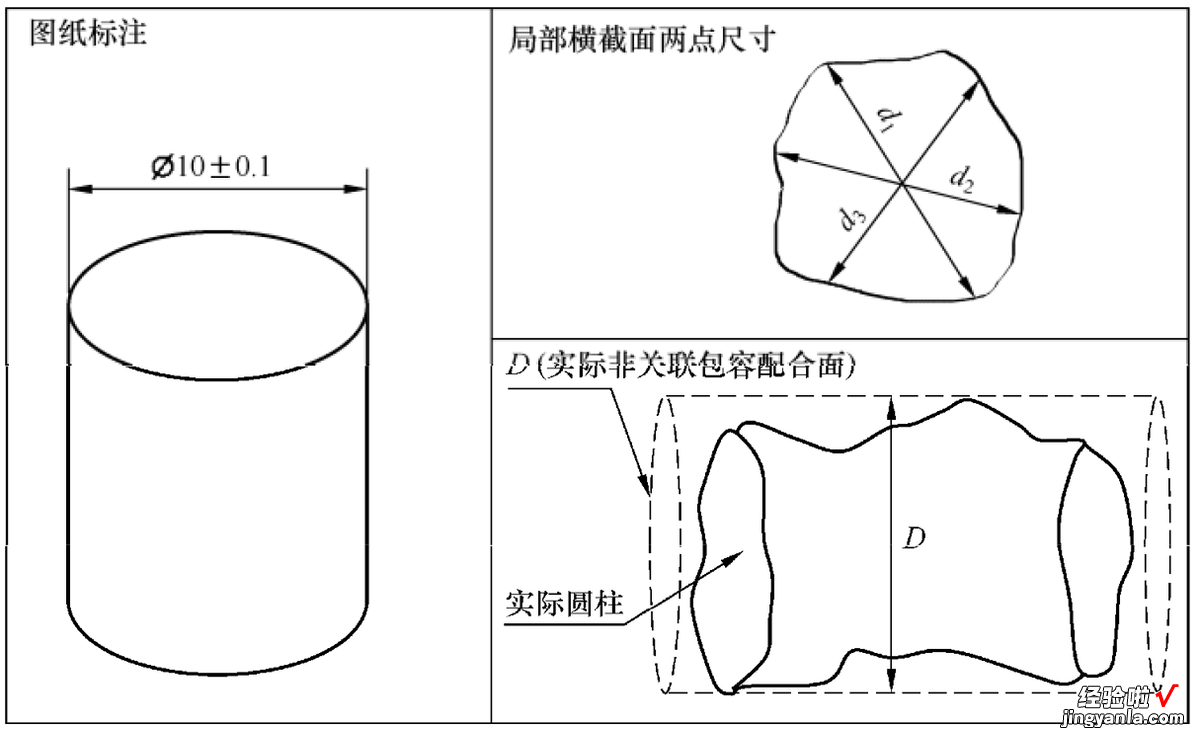
图 1?44轴的包容原则检测标注示例
孔的包容原则检测标注示例如图1?46所示,图中的孔,非关联实际包容配合面的尺寸要大于或等于最大实体包容边界尺寸7.8,实际局部横截面两点尺寸也不能超出图纸标注的尺寸公差范围 。
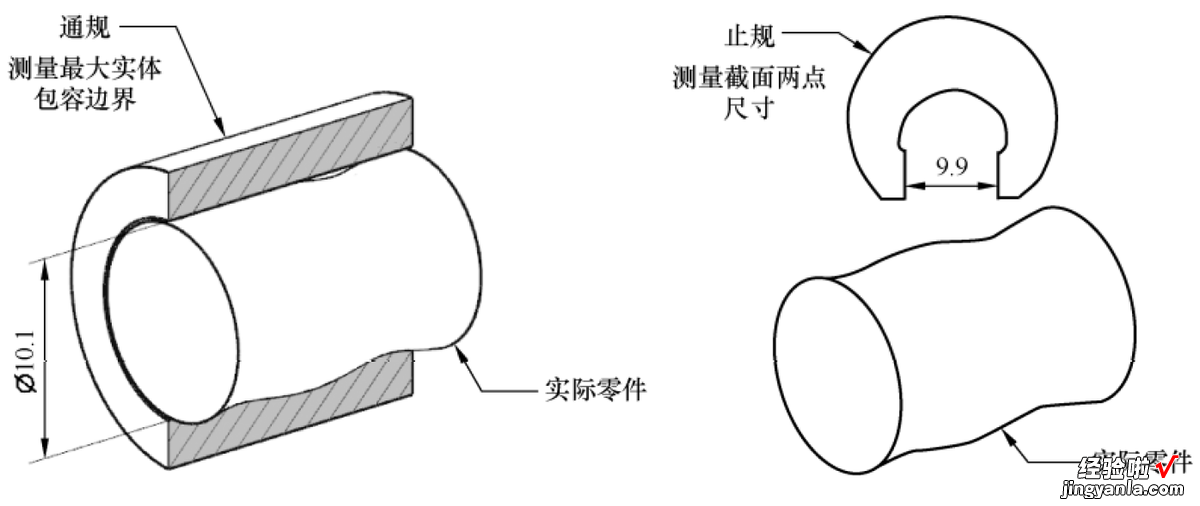
图 1?45轴的包容原则检测之通止规法标注示例
可以采用通止规法检测图1?46所示孔的尺寸,通规检验零件非关联实际包容配合面尺寸要大于或等于最大实体包容边界,通规圆柱直径尺寸是7.8,通规的长度应该大于或等于孔的长度尺寸,只要?7.8的通规通过实际孔,就表示孔的实际表面没有超过最大实体包容边界 。止规检测零件实际局部尺寸,止规尺寸是8.2,只要止规不能通过实际孔,就表示孔的实际局部尺寸合格,止规理论上应该是两点法测量 。
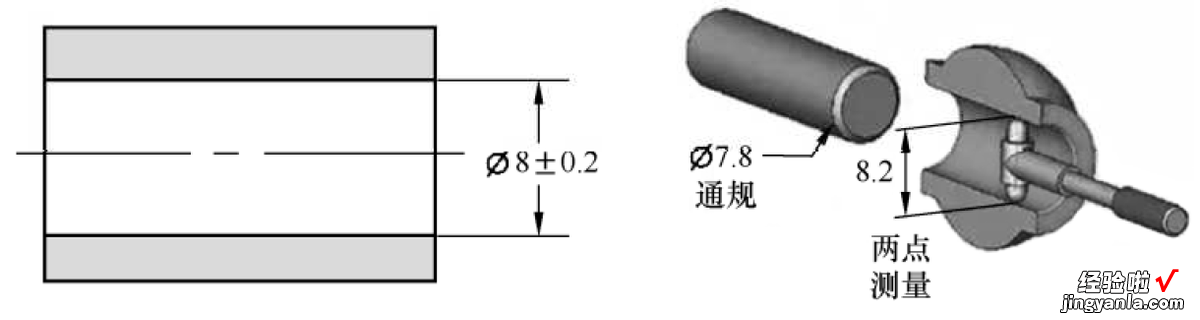
图 1?46孔的包容原则检测标注示例
包容原则的失效
以下几种情况可以不遵循包容原则的要求,即规则尺寸要素在最大实体时,形状不需要保持理想状态 。
(1)公差采用自由状态修饰符号 。
(2)标准零件的尺寸 , 如棒、管路、板件等,这些零件在加工前首先要满足相应的标准规范中规定的几何特征要求 。
(3)在尺寸公差后面加上独立符号 , 表示公差原则采用独立原则 。
(4)直线度管控规则尺寸要素形状误差,如中心线的直线度 。
(5)平面度管控规则尺寸要素形状误差,如中心面的平面度 。
(6)采用平均直径标注 。
包容原则失效标注示例如图1?47所示 。在图1?47的(a)中,圆度公差后面有修饰符号,表示自由状态,可以不遵循包容原则要求,即圆度公差值可以大于尺寸公差值 。
在图1?47的(b)中,尺寸公差后面标注表示公差原则采用独立原则,形状公差可以大于尺寸公差,可以不遵循包容原则要求 。在图1?47的(c)中,直线度管控轴的中心线的形状误差,图纸标注表示即使轴在最大实体(MMC)时 , 也可以有0.6的形状误差 , 不需要保持形状理想状态,可以不遵循包容原则要求 。在图1?47的(d)中,平面度管控板的中心面的形状误差,图纸标注表示即使板在最大实体(MMC)时,也可以有0.6的形状误差,不需要保持形状理想状态,可以不遵循包容原则要求 。在图1?47的(e)中,在尺寸后面加AVG表示平均尺寸 , 可以不遵循包容原则 。
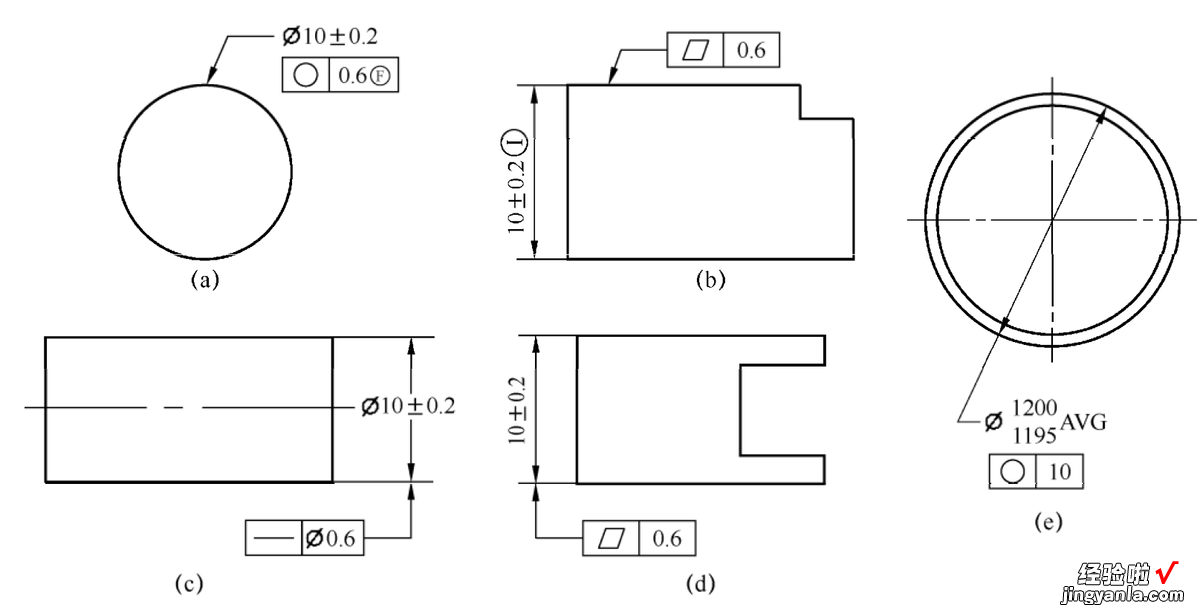
图 1?47包容原则失效标注示例
独立原则
独立原则解释了尺寸公差和形状公差之间的关系,当规则尺寸要素 , 如孔和轴不用来配合,默认的包容原则加严了设计要求,增加了产品成本 。此时应该采用独立原则要求 , 独立原则是通过在尺寸公差后面标注来表达的 。独立原则解释如下:图样上给定的每个尺寸和形状、方向和位置是独立的,应分别满足要求,在独立原则下,图纸标注的尺寸公差只控制局部实际尺寸,即任意一个横截面局部两点之间的尺寸,不控制要素本身的形状误差 。比如 , 圆柱的直径公差,只管控圆柱每个截面的局部实际尺寸,不管控圆柱的形状(即直线度或圆柱度及截面的圆度)误差 。独立原则下,轴的尺寸和形状关系标注示例如图1?48独立原则下,轴的尺寸和形状关系标注示例所示 。图1?48独立原则下,轴的尺寸和形状关系标注示例中的圆柱不需要在最大实体时形状保持理想状态,即使每个横截面的尺寸都等于最大实体尺寸8.2,轴也可以弯曲 , 即允许有形状误差 。因为在独立原则下,轴的尺寸是不管控形状误差的,产品检测也不会去测量形状误差,只要测量任意一个横截面两点之间的尺寸在图纸允许的尺寸公差范围内就算合格 。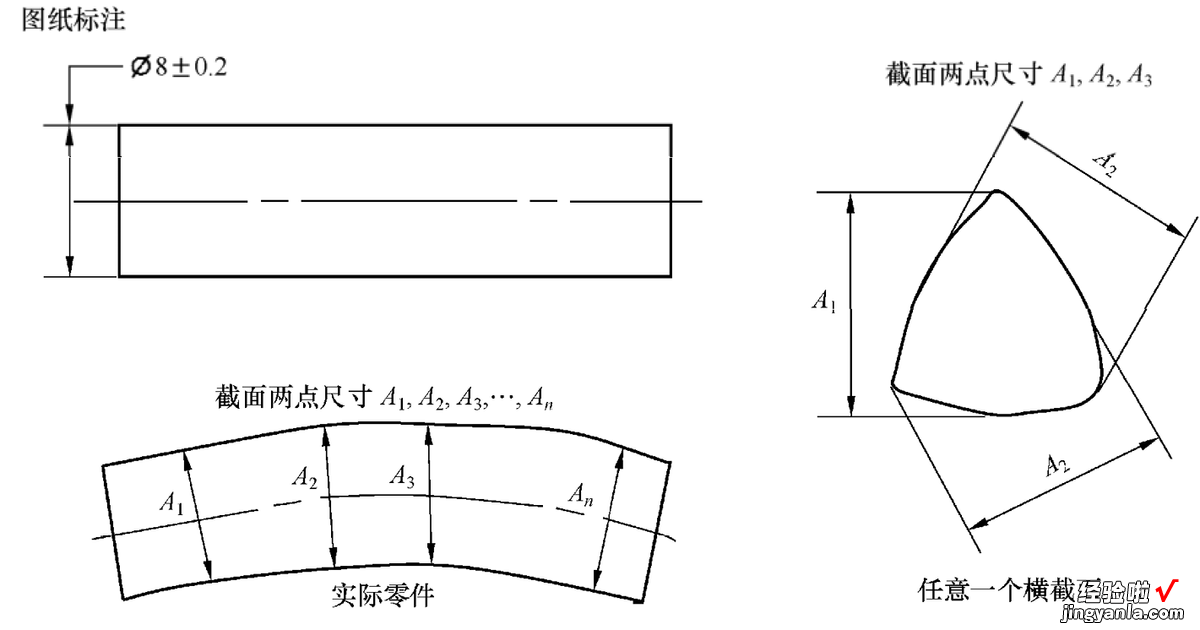
图 1?48独立原则下,轴的尺寸和形状关系标注示例
独立原则的特点如下:
(1)尺寸公差仅控制要素的局部实际尺寸,不控制其形状公差 。
(2)形状公差可以大于或小于尺寸公差 。
(3)产品检测时,尺寸公差采用两点法检测(卡尺法) 。
独立原则的应用如下:
1.没有配合要求的情况
零件外形尺寸、管路尺寸 , 以及工艺结构尺寸,如退刀槽尺寸、螺纹收尾、倒圆、倒角尺寸等 。一些不需要配合的孔和轴的尺寸,如工艺孔、排气孔等 。
2.配合精度要求不高的情况孔和轴配合,但配合间隙比较大,如最小直径为12的孔和最大直径为10的轴装配,即使孔和轴在最大实体时 , 孔和轴有一点弯曲变形即形状不理想也可以装配 。
独立原则的检测:
独立原则只需要两点法测量实际局部尺寸(如游标卡尺、内径千分尺),实际局部尺寸不要超过图纸标注的公差即可 。独立原则检测标注示例如图1?49独立原则检测标注示例所示,图中的d1~d3要在尺寸公差?10±0.1范围内 。

【公差的基本符号及基本原则】图 1?49独立原则检测标注示例
