写在前面
什么是描述性统计分析 , 这不仅是数据分析面试中最常见的问题 , 也是我们日常分析中必过的一道关卡 。要把握数据的分布特征,需要从3个方面进行描述:集中趋势、离散程度和分布形状 。
1、集中趋势
集中趋势就是指一组数据向某一中心靠拢的程度,通常有以下指标:众数
对分类数据来说 , 众数是最适合描述其集中趋势的值,它是指一组数据中出现次数最多的变量,众数不受极端值的影响,但是可能不唯一 , 且当数据量较多时,才有意义 。中位数
对数据型数据来说 , 可以用中位数来描述其集中趋势的度量,中位数就是将一组数据排序以后处于中间位置的值,那么如何寻找中间位置呢?1、 将这组数据按顺序排列2、 中间数值所在的位置是(n 1)/2,n表示n个数3、 当n为奇数时,中间位置的数就是中位数 , 当n为偶数时,中间位置两个数的均值为中位数 。
显然这里有两种情况,当n为奇数和偶数两种情况 , 求下面这组数据的中位数
0 1 2 3 4 5 6 7 8这里n=9,中位数的位置=(9 1)/2 = 5,那么中位数就是4.
0 1 2 3 4 5 6 7 8 9当n=10时,中位数的位置是 (10 1)/2 = 5.5,那么中位数就是第5个位置的数和第6个位置的数的平均数,也就是(4 5)/2 = 4.5
知道计算的原理,但其实不用我们自己去算,软件中有相应的函数,如Excel中的median函数可以计算中位数 。中位数也不受极值的影响 。
四分位数
同样 , 四分位数也是对数值型数据集中趋势的度量 , 后面的度量都适用于数值型数据 。四分位数就是将数据排序后四等分,处于25%(下四分位数)和75%(上四分位数)位置上的值即四分位数,箱型图可以很好地用来描述四分位数 。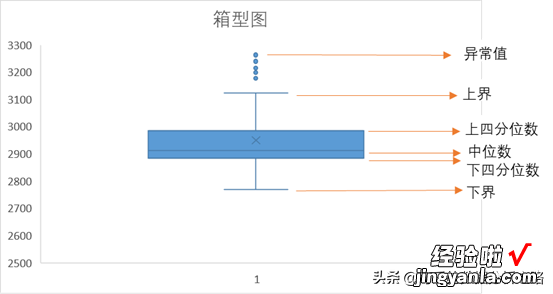
【Excel描述分析怎么做 如何做好描述统计分析】Excel中可以用quartile函数来计算四分位数 。
平均数
简单平均数:就是算术平均数,所有数值相加再除以总个数 。加权平均数:数据分组后每组有相应的权重 。几何平均数:n个变量乘积的n次方根 , 主要用于计算平均比率,如增长率的平均值 。Excel中用average函数计算平均数 。
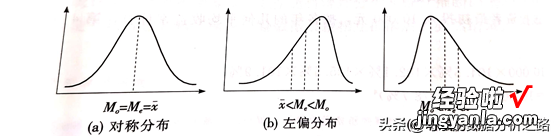
如果分布是对称的,那么众数=中位数=平均数,如果数据左偏 , 那么平均数<中位数<众数,如果数据右偏,那么众数<中位数<平均数 , 根据数据的分布形态,选择适合的集中趋势度量去描述 。
2、离散程度
离散程度就是描述各个变量远离其中心值的程度 , 通常有以下指标:异众比率
指非众数组的频数占总频数的比例,较多地用在分类数据中 , 用来体现众数的代表性 。异众比率越大,说明非众数组占比越大,那么众数就不能很好地代表这组数据 。四分位差
对于数值型数据,四分位差可以来描述数据的离散程度,四分位差就是上下四分位数的差 。反映了中间50%数据的离散程度,四分位差越?。?说明中间的数据越集中,极差
极差就是最大值与最小值的差,容易受极值的影响 。平均差
各变量与其平均数离差绝对值的平均数,反映了每个数与平均数的差异程度,Excel里用avedev计算平均差 。方差和标准差
对数值型数据,怎么能少得了我们熟知的方差和标准差 。方差就是各变量与其平均数离差平方的平均数,方差的平方根就是标准差,方差和标准差是应用最广的描述数据离散程度的度量 。Excel里用stdev来计算标准差 。3、分布形状
描述分布形状的度量有偏态和峰态偏态
数据分布对称性的描述 , 统计量是偏度,偏度>0,则频数分布的高峰向左偏移 , 呈右(正)偏态分布;偏度<0,则频数分布的高峰向右偏移,呈左(负)偏态分布;|偏度|>1,呈高度偏态 , 0.5<|偏度|<1,呈中等偏态,一个记忆方法就是,尾巴在哪边就是哪偏 。对于偏态,在之前的文章 中也有写过 。如何处理偏态数据?
峰态
是描述数据平峰或尖峰程度的度量 。统计量是峰度 。同偏态一样,峰态也是与标准正态分布来比较的 , 峰度>0,数据分布更集中 , 为尖峰分布,峰度<0,数据分布更分散 , 为平峰分布 。以上提到的各种统计量除了用Excel中的函数来计算外,还可直接用【数据分析】功能中的【描述统计】命令直接得到 。
猜你喜欢:
泰坦尼克号数据分析案例实战
数据分析有哪些岗位?

